
| C | f(1) n |
| C | f(2) n |
| C | f(3) n |
| C | f(2n) n |
| 2n |
 |
| k=1 |
| C | f(k) n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n-1 n |
| 2n |
 |
| k=1 |
| C | f(k) n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n-1 n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n-1 n |
| C | n n |


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
|
| a |
| an |
查看答案和解析>>
科目:高中数学 来源: 题型:013
下列说法正确的是
[
]A
.数列可以看做是一个定义域为正整数集N*的函数B
.数列可以看做是一个定义域为正整数集N*(或它的有限子集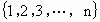 )的函数,当自变量从小到大依次取值时对应的一列函数值
)的函数,当自变量从小到大依次取值时对应的一列函数值
C
.数列可以看做是一个定义域为正整数集N*(或它的有限子集)的函数D
.数列可以看做是一个定义域为正整数集N*(或它的有限子集)的函数值查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
下列说法正确的是
[ ]
A.数列可以看做是一个定义域为正整数集N*的函数
B.数列可以看做是一个定义域为正整数集N*(或它的有限子集 )的函数,当自变量从小到大依次取值时对应的一列函数值
)的函数,当自变量从小到大依次取值时对应的一列函数值
C.数列可以看做是一个定义域为正整数集N*(或它的有限子集)的函数
D.数列可以看做是一个定义域为正整数集N*(或它的有限子集)的函数值
查看答案和解析>>
科目:高中数学 来源:天津市新人教A版数学2012届高三单元测试13:等差数列 新人教A版 题型:013
下列说法正确的是
A.数列1,3,5,7可表示为{1,3,5,7}
B.数列1,0,-1,-2与数列―2,―1,0,1是相同的数列
C.数列![]() 的第k项是
的第k项是![]()
D.数列可以看做是一个定义域为正整数集N*的函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com