
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 有两个大于
有两个大于![]() 的零点,求
的零点,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】 山东省《体育高考方案》于2012年2月份公布,方案要求以学校为单位进行体育测试,某校对高三1班同学按照高考测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
(Ⅰ)请估计一下这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成一个小组.若选出的两人成绩差大于20,则称这两人为“帮扶组”,试求选出的两人为“帮扶组”的概率.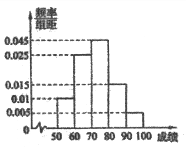
查看答案和解析>>
科目:高中数学 来源: 题型:
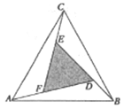
【题目】赵爽是我国古代数学家、天文学家,大约在公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽炫图”(以弦为边长得到的正方形组成).类比“赵爽弦图”,可类似地构造如下图所示的图形,它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形,设![]() ,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是__________.
,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级共有学生![]() 名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为
名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为![]() 分)进行统计,绘制出如下尚未完成的频率分布表:
分)进行统计,绘制出如下尚未完成的频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
|
| |
| ||
|
|
(1)补充完整题中的频率分布表;
(2)若成绩在![]() 为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.
为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).M是曲线
为参数).M是曲线![]() 上的动点,将线段OM绕O点顺时针旋转
上的动点,将线段OM绕O点顺时针旋转![]() 得到线段ON,设点N的轨迹为曲线
得到线段ON,设点N的轨迹为曲线![]() .以坐标原点O为极点,
.以坐标原点O为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,若射线![]() 与曲线
与曲线![]() 分别交于A, B两点(除极点外),且有定点
分别交于A, B两点(除极点外),且有定点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村电费收取有以下两种方案供农户选择:
方案一:每户每月收取管理费2元,月用电量不超过30度时,每度0.5元;超过30度时,超过部分按每度0.6元收取:
方案二:不收取管理费,每度0.58元.
(1)求方案一的收费L(x)(元)与用电量x(度)间的函数关系.若老王家九月份按方案一缴费35元,问老王家该月用电多少度?
(2)老王家该月用电量在什么范围内,选择方案一比选择方案二好?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com