练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设圆C1：x2+y2﹣10x+4y+25＝0与圆C2：x2+y2﹣14x+2y+25＝0，点A，B分别是C1，C2上的动点，M为直线y＝x上的动点，则|MA|+|MB|的最小值为（　　）

    A.3B.3C.5D.5

    【答案】B

    【解析】

    根据圆的方程可以求出圆心和半径，所以|MA|+|MB|，即只需求的最小值，根据平面对称知识即可求出．

    圆C1：x2+y2﹣10x+4y+25＝0即，所以圆心，半径为2，

    圆C2：x2+y2﹣14x+2y+25＝0即，所以圆心，半径为5，

    由圆的几何性质可知，|MA|+|MB|，

    即求出的最小值可得|MA|+|MB|的最小值．

    因为点关于直线y＝x的对称点为，所以当共线时，

    的最小值为．

    故|MA|+|MB|的最小值为3．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为了引导居民合理用电，国家决定实行合理的阶梯电价，居民用电原则上以住宅为单位（一套住宅为一户）.

    阶梯级别

    第一阶梯

    第二阶梯

    第三阶梯

    月用电范围（度）

    （0,210]

    （210,400]

    某市随机抽取10户同一个月的用电情况，得到统计表如下：

    居民用电户编号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    用电量（度）

    53

    86

    90

    124

    132

    200

    215

    225

    300

    410

    若规定第一阶梯电价每度0.5元，第二阶梯超出第一阶梯的部分每度0.6元，第三阶梯超出第二阶梯的部分每度0.8元，试计算A居民用电户用电410度时应电费多少元？

    现要在这10户家庭中任意选取3户，求取到第二阶梯电量的户数的分布列与期望；

    以表中抽到的10户作为样本估计全市的居民用电，现从全市中依次抽取10户，若抽到户用电量为第一阶梯的可能性最大，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某绿色有机水果店中一款有机草莓味道鲜甜，店家每天以每斤元的价格从农场购进适量草莓，然后以每斤元的价格出售，如果当天卖不完，剩下的草莓由果汁厂以每斤元的价格回收.

    （1）若水果店一天购进斤草莓，求当天的利润（单位：元）关于当天需求量（单位：斤，）的函数解析式；

    （2）水果店记录了天草莓的日需求量（单位：斤），整理得下表：

    日需求量

    14

    15

    16

    17

    18

    19

    20

    频数

    14

    22

    14

    16

    15

    13

    6

    ①假设水果店在这天内每天购进斤草莓，求这天的日利润（单位：元）的平均数；

    ②若水果店一天购进斤草莓，以天记录的各需求量的频率作为各需求量发生的概率，求当天的利润不少于元的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数为R上的偶函数，当时当时，且对恒成立，函数的一个周期内的图像与函数的图像恰好有两个公共点，则 （ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】两圆(圆心,半径),与(圆心,半径)不是同心圆,方程相减(消去二次项)得到的直线叫做圆 与圆的根轴;

    (1)求证:当与相交于A,B两点时,所在直线为根轴;

    (2)对根轴上任意点P,求证:;

    (3)设根轴与交于点H,,求证:H分的比;

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司租赁甲、乙两种设备生产、两类产品，甲种设备每天能生产类产品件和类产品件，乙种设备每天能生产类产品件和类产品件．已知设备甲每天的租赁费为元，设备乙每天的租赁费为元，现该公司至少要生产类产品件，类产品件，求所需租赁费最少为多少元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司租赁甲、乙两种设备生产、两类产品，甲种设备每天能生产类产品件和类产品件，乙种设备每天能生产类产品件和类产品件．已知设备甲每天的租赁费为元，设备乙每天的租赁费为元，现该公司至少要生产类产品件，类产品件，求所需租赁费最少为多少元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC﹣A1B1C1中，点D、E、F分别为线段A1C1、AB、A1A的中点，A1A＝AC＝BC，∠ACB＝90°．求证：

    （1）DE∥平面BCC1B1；

    （2）EF⊥平面B1CE．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】直角坐标系xOy中，点A坐标为(2,0)，点B坐标为(4,3)，点C坐标为(1,3)，且（t∈R）.

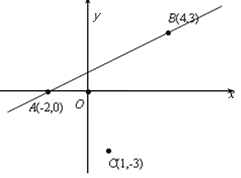
    (1) 若CM⊥AB，求t的值；

    (2) 当0≤ t ≤1时，求直线CM的斜率k和倾斜角θ的取值范围.

    查看答案和解析>>

    同步练习册答案