Question

20.已知二次函数y=f₁(x)的图象以原点为顶点且过点(1，1)，反比例函数y=f₂(x)的图象与直线y=x的两个交点间距离为8,f(x)=f₁(x)+f₂(x).

(1)求函数f(x)的表达式；

(2)证明：当a＞3时，关于x的方程f(x)=f(a)有三个实数解.

Answer 1

20. [解] (1)由已知，设f₁(x)=ax²,由f₁(1)=1,得a=1，∴f₁(x)=x².

设f₂(x)=(k＞0)，它的图象与直线y=x的交点分别为

A(,),B(－,－),

由|AB|=8，得k=8,∴f₂(x)=.

故f(x)=x²+.

(2) [证法一]由f(x)=f(a)得x²+=a²+,

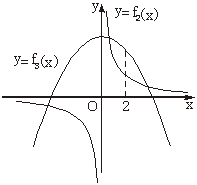
即=－x²+a²+.

在同一坐标系内作出f₂(x)=和f₃(x)=－x²+a²+的大致图象，其中f₂(x)的图象是以坐标轴为渐近线，且位于第一、三象限的双曲线，f₃(x)的图象是以(0,a²＋)为顶点，开口向下的抛物线.

因此，f₂(x)与f₃(x)的图象在第三象限有一个交点，

即f(x)=f(a)有一个负数解.

又∵f₂(2)=4，f₃(2)=a²+－4,

当a＞3时，f₃(2)－f₂(2)=a²+－8＞0,

∴当a＞3时，在第一象限f₃(x)的图象上存在一点(2，f₃(2))在f₂(x)图象的上方.

∴f₂(x)与f₃(x)的图象在第一象限有两个交点，即f(x)=f(a)有两个正数解.因此，方程f(x)=f(a)有三个实数解.

[证法二]由f(x)=f(a)，得x²+=a²+，

即(x－a)(x+a－)=0，得方程的一个解x₁=a.

方程x+a－=0化为ax²+a²x－8=0,

由a＞3，Δ=a⁴+32a＞0，得

x₂=，x₃=.

∵x₂＜0，x₃＞0,∴x₂≠x₁,且x₂≠x₃.

若x₁=x₃,即a=,

则3a²=,a⁴=4a,

得a=0或a=,这与a＞3矛盾，∴x₁≠x₃.

故原方程有三个实数解.