
【题目】已知复数z=(2m2+3m﹣2)+(m2+m﹣2)i,(m∈R)根据下列条件,求m值.
(1)z是实数;
(2)z是虚数;
(3)z是纯虚数;
(4)z=0.
【答案】
(1)解:当m2+m﹣2=0,即m=﹣2或m=1时,z为实数
(2)解:当m2+m﹣2≠0,即m≠﹣2且m≠1时,z为虚数
(3)解:当 ![]() ,解得m=
,解得m= ![]() ,
,
即 m= ![]() 时,z为纯虚数
时,z为纯虚数
(4)解:令 ![]() ,解得 m=﹣2,即m=﹣2时,z=0
,解得 m=﹣2,即m=﹣2时,z=0
【解析】(1)当复数的虚部等于零时,复数为实数,由此求得m的值.(2)当复数的虚部不等于零时,复数为虚数,由此求得m的值.(3)当复数的实部等于零,且虚部不等于零时,复数为纯虚数,由此求得m的值.(4)当复数的实部等于零,且虚部也等于零时,复数等于零,由此求得m的值.
【考点精析】掌握复数的定义和复数相等是解答本题的根本,需要知道形如![]() 的数叫做复数,
的数叫做复数,![]() 和
和![]() 分别叫它的实部和虚部;如果两个复数实部相等且虚部相等就说这两个复数相等.
分别叫它的实部和虚部;如果两个复数实部相等且虚部相等就说这两个复数相等.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】观察以下三个等式: sin215°﹣sin245°+sin15°cos45°=﹣ ![]() ,
,
sin220°﹣sin250°+sin20°cos50°=﹣ ![]() ,
,
sin230°﹣sin260°+sin30°cos60°=﹣ ![]() ;
;
猜想出一个反映一般规律的等式: .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量m=(3sinx,cosx),n=(-cosx,![]() cosx),f(x)=m·n-
cosx),f(x)=m·n-![]() .
.
(1)求函数f(x)的最大值及取得最大值时x的值;
(2)若方程f(x)=a在区间![]() 上有两个不同的实数根,求实数a的取值范围.
上有两个不同的实数根,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在[﹣1,1]的函数f(x)满足下列两个条件:①任意的x∈[﹣1,1],都有f(﹣x)=﹣f(x);②任意的m,n∈[0,1],当m≠n,都有 ![]() <0,则不等式f(1﹣3x)<f(x﹣1)的解集是( )
<0,则不等式f(1﹣3x)<f(x﹣1)的解集是( )
A.[0, ![]() )
)
B.( ![]() ,
, ![]() ]
]
C.[﹣1, ![]() )
)
D.[ ![]() ,1]
,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】放射性元素由于不断有原子放射出微粒子而变成其他元素,其含量不断减少,这种现象称为衰变.假设在放射性同位素铯137的衰变过程中,其含量M(单位:太贝克)与时间t(单位:年)满足函数关系:M(t)=M0 ![]() ,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是﹣10In2(太贝克/年),则M(60)=( )
,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是﹣10In2(太贝克/年),则M(60)=( )
A.5太贝克
B.75In2太贝克
C.150In2太贝克
D.150太贝克
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ax3+bx2+cx的极小值为﹣8,其导函数y=f′(x)的图象经过点 ![]() ,如图所示,
,如图所示, 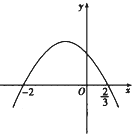
(1)求f(x)的解析式;
(2)若对x∈[﹣3,3]都有f(x)≥m2﹣14m恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=x3+ax2+bx+1的导函数f′(x)满足f′(x)=2a,f′(2)=﹣b,
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)设g(x)=f′(x)ex , 求函数g(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(﹣1,1)上的减函数f(x)且满足对任意的实数x,y都有f(x+y)=f(x)+f(y)
(Ⅰ)判断函数f(x)的奇偶性;
(Ⅱ)解关于x的不等式f(log2x﹣1)+f(log2x)<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com