
【题目】
近年来,随着双十一、双十二等网络活动的风靡,各大网商都想出了一系列的降价方案,以此来提高自己的产品利润. 已知在2016年双十一某网商的活动中,某店家采取了两种优惠方案以供选择:
方案一:购物满400元以上的,超出400元的部分只需支出超出部分的x%;
方案二:购物满400元以上的,可以参加电子抽奖活动,即从1,2,3,4,5,6这6张卡牌中任取2张,将得到的数字相加,所得结果与享受优惠如下:
数字和 | [3,4] | [5,7] | [8,9] | [10,11] |
实际付款 | 原价 | 9折 | 8折 | 5折 |
(Ⅰ)若某顾客消费了800元,且选择方案二,求该顾客只需支付640元的概率;
(Ⅱ)若某顾客购物金额为500元,她选择了方案二后,得到的数字之和为6,此时她发现使用方案一、二最后支付的金额相同,求x的值.
【答案】(1) ![]() (2)50
(2)50
【解析】试题分析:(1) 该顾客花了640元,说明所取数字之和在[8,9]之间,故满足条件的为(3,5),(3,6),(4,5),(2,6),总的事件个数为15,从而得到所求概率;(2) 依题意,该顾客需要支付450元,故400+x%×100=450,解得x=50.
试题解析:
依题意,所有的情况为(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6).
(Ⅰ)若该顾客花了640元,说明所取数字之和在[8,9]之间,故满足条件的为(3,5),(3,6),(4,5),(2,6),所求概率为![]() .
.
(Ⅱ)依题意,该顾客需要支付450元,故400+x%×100=450,解得x=50.


科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC-A1B1C1中,平面α与棱AB,AC,A1C1,A1B1分别交于点E,F,G,H,且直线AA1∥平面α.有下列三个命题:①四边形EFGH是平行四边形;②平面α∥平面BCC1B1;③平面α⊥平面BCFE.其中正确的命题有( )
A. ①② B. ②③
C. ①③ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是各项均为正数的等比数列,且b1=a1=1,b3=a4,b1+b2+b3=a3+a4.
(1)求数列{an},{bn}的通项公式;
(2)设cn=anbn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为D,如果x∈D,y∈D,使得f(x)=-f(y)成立,则称函数f(x)为“Ω函数”.给出下列四个函数:①y=sin x;②y=2x;③y=![]() ;④f(x)=ln x.则其中“Ω函数”共有( )
;④f(x)=ln x.则其中“Ω函数”共有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项都为正数的数列{an}满足a1=1, ![]() =2an+1(an+1)-an.
=2an+1(an+1)-an.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=![]() ,求数列{an·bn}的前n项和Tn.
,求数列{an·bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等差数列,a10=4a3,a4=3a1+7.
(1)求通项公式an;
(2)若bn=an-2an+2,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
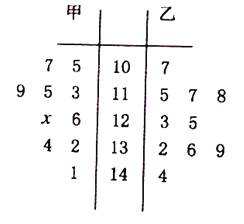
【题目】为了减少雾霾,还城市一片蓝天,某市政府于12月4日到12月31日在主城区实行车辆限号出行政策,鼓励民众不开车低碳出行,某甲乙两个单位各有200名员工,为了了解员工低碳出行的情况,统计了12月5日到12月14日共10天的低碳出行的人数,画出茎叶图如下:
(1)若甲单位数据的平均数是122,求![]() ;
;
(2)现从如图的数据中任取4天的数据(甲、乙两单位中各取2天),记其中甲、乙两单位员工低碳出行人数不低于130人的天数为![]() ,
, ![]() ,令
,令![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com