
【题目】如图,焦点在x轴的椭圆,离心率e= ![]() ,且过点A(﹣2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线y=1反射后交椭圆于Q点(Q点与P点不重合).
,且过点A(﹣2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线y=1反射后交椭圆于Q点(Q点与P点不重合).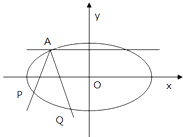
(1)求椭圆标准方程;
(2)求证:直线PQ的斜率为定值;
(3)求△OPQ的面积的最大值.
【答案】
(1)解:设椭圆方程为 ![]() ,
,
∵椭圆经过点(﹣2,1),
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∴椭圆方程为 ![]()
(2)证明:设直线AP方程为y=k(x+2)+1,则直线AQ的方程为y=﹣k(x+2)+1
由 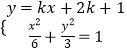 可得(1+2k2)x2+4k(2k+1)x+8k2+8k﹣4=0,△>0,
可得(1+2k2)x2+4k(2k+1)x+8k2+8k﹣4=0,△>0,
设P(x1,y1),由A(﹣2,1)可得 ![]() ,
,
∴P( ![]() ,
, ![]() ),
),
同理可得Q( ![]() ,
, ![]() ),
),
∴kPQ=﹣1
(3)由(2),设PQ的方程为y=﹣x+m,代入椭圆方程得:3x2﹣4mx+2m2﹣6=0.
令△>0,得﹣3<m<3,
设P(x1,y1),Q(x2,y2),则 ![]() ,
,
∴ ![]()
设原点O到直线的距离为d,则 ![]() ,
,
∴ ![]() ,
,
当 ![]() 时,△OPQ面积的最大值为
时,△OPQ面积的最大值为 ![]()
【解析】(1)设出椭圆的方程利用离心率且过点A求出几何量即可得出椭圆的标准方程。(2)设出直线的方程分别与椭圆的方程联立,求出P、Q的坐标即可得出结论。(3)根据题意设出PQ的直线方程代入椭圆方程利用弦长公式求出![]() 再求出原点到直线的距离即可得△OPQ的面积,然后利用基本不等式即可求出最大值。
再求出原点到直线的距离即可得△OPQ的面积,然后利用基本不等式即可求出最大值。


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1 , l2 , 直线l1与C交于A、B两点,直线l2与C交于D、E两点,则|AB|+|DE|的最小值为( )
A.16
B.14
C.12
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,
, ![]() 是非零不共线的向量,设
是非零不共线的向量,设 ![]() =
= ![]() +
+ ![]() ,定义点集M={K|
,定义点集M={K| ![]() =
= ![]() },当K1 , K2∈M时,若对于任意的r≥2,不等式|
},当K1 , K2∈M时,若对于任意的r≥2,不等式| ![]() |≤c|
|≤c| ![]() |恒成立,则实数c的最小值为 .
|恒成立,则实数c的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设复平面上点Z1 , Z2 , …,Zn , …分别对应复数z1 , z2 , …,zn , …;
(1)设z=r(cosα+isinα),(r>0,α∈R),用数学归纳法证明:zn=rn(cosnα+isinnα),n∈Z+
(2)已知 ![]() ,且
,且 ![]() (cosα+isinα)(α为实常数),求出数列{zn}的通项公式;
(cosα+isinα)(α为实常数),求出数列{zn}的通项公式;
(3)在(2)的条件下,求 ![]() |+….
|+….
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆x2+y2=12与抛物线x2=4y相交于A,B两点,F为抛物线的焦点,若过点F且斜率为1的直线l与抛物线和圆交于四个不同的点,从左至右依次为P1 , P2 , P3 , P4 , 则|P1P2|+|P3P4|的值 , 若直线m与抛物线相交于M,N两点,且与圆相切,切点D在劣弧 ![]() 上,则|MF|+|NF|的取值范围是 .
上,则|MF|+|NF|的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+1)﹣x2+(2﹣a)x﹣a(a∈R)若存在唯一的正整数x0 , 使得f(x0)>0,则实数a的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() ]
]
D.(ln3,ln2+1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ln(x+m)﹣nlnx.
(1)当m=1,n>0时,求函数f(x)的单调减区间;
(2)n=1时,函数g(x)=(m+2x)f(x)﹣am,若存在m>0,使得g(x)>0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.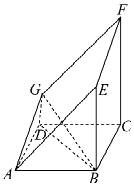
(1)求证:BD⊥平面ADG;
(2)求直线GB与平面AEFG所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com