Question

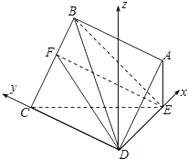
【题目】边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD，且AE⊥平面CDE，AE=1．

（1）求证：平面ABCD⊥平面ADE；
（2）设点F是棱BC上一点，若二面角A﹣DE﹣F的余弦值为 ，试确定点F在BC上的位置．

Answer 1

【答案】
（1）证明：∵AE⊥平面CDE，∴AE⊥CD，

又∵AD⊥CD，AE∩AD=A，

∴CD⊥面ADE，

又CD面ABCD，

∴平面ABCD⊥平面ADE．

（2）解：∵CD⊥DE，

∴如图，以D为原点，DE为x轴，DC为y轴，过D作平面CDE的垂线为z轴，

建立空间直角坐标系D﹣xyz，

则： ，

∴ ，∴ ，

设 ，λ∈[0，1]

则 …（10分）

设平面FDE的法向量为 ，

则 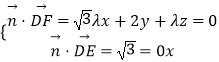，取z=﹣2，得 ，

又平面ADE的法向量为 ，

∴ ，∴ ，

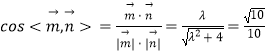故当点F满足 时，二面角A﹣DE﹣F的余弦值为

【解析】（1）推导出AE⊥CD，AD⊥CD，得CD⊥面ADE，由此能证明平面ABCD⊥平面ADE．（2）以D为原点，DE为x轴，DC为y轴，过D作平面CDE的垂线为z轴，建立空间直角坐标系D﹣xyz，利用向量法能求出当点F满足 时，二面角A﹣DE﹣F的余弦值为 ．
【考点精析】认真审题，首先需要了解平面与平面垂直的判定(一个平面过另一个平面的垂线，则这两个平面垂直)．