
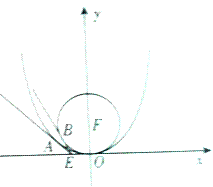
【题目】如图所示,抛物线C:x2=2py(p>0),其焦点为F,C上的一点M(4,m)满足|MF|=4.
(1)求抛物线C的标准方程;
(2)过点E(﹣1,0)作不经过原点的两条直线EA,EB分别与抛物线C和圆F:x2+(y﹣2)2=4相切于点A,B,试判断直线AB是否经过焦点F.
【答案】(1)x2=8y(2)直线AB的方程为![]() ,经过焦点F(0,2)
,经过焦点F(0,2)
【解析】试题分析:(1)由点M(4,m)在抛物线上得16=2pm,根据抛物线的定义得|MF|=m+![]() =4,建立关于p的方程求得p即可得到所求方程;(2)设出直线EA,EB的方程,根据相切利用代数方法求得切点A,B的坐标,然后求得直线AB的方程后验证即可。
=4,建立关于p的方程求得p即可得到所求方程;(2)设出直线EA,EB的方程,根据相切利用代数方法求得切点A,B的坐标,然后求得直线AB的方程后验证即可。
试题解析:
(1)由条件得抛物线C的准线方程为![]() ,
,
∴|MF|=m+![]() =4,
=4,
∵点M(4,m)在抛物线上,
∴16=2pm,
∴p2﹣8p+16=0,解得p=4,
∴抛物线C的标准方程为x2=8y。
(2)设直线EA的方程为![]() ,
,
由![]() ,消去x整理得得
,消去x整理得得![]() 2y2﹣(2
2y2﹣(2![]() +8)y+1=0,
+8)y+1=0,
∵直线EA与抛物线C相切,
∴△=(2![]() +8)2﹣4
+8)2﹣4![]() 2=0,解得
2=0,解得![]() =﹣2,
=﹣2,
∴![]() y2﹣4y+1=0
y2﹣4y+1=0
解得![]()
∴![]() ,
,
故点A的坐标为![]() ,
,
设直线EB的方程为x=ty﹣1,
由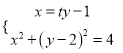 ,消去x整理得:(t2+1)y2﹣(2t+4)y+1=0,
,消去x整理得:(t2+1)y2﹣(2t+4)y+1=0,
∵直线EB与圆F相切,
∴△=(2t+4)2﹣4(t2+1)=0,解得![]() ,
,
∴25y2﹣40y+16=0
解得y![]() ,
,
![]() ,
,
故点B的坐标为![]() ,
,
∴直线AB的斜率![]() ,
,
可得直线AB的方程为![]() ,该直线经过抛物线的焦点F(0,2)。
,该直线经过抛物线的焦点F(0,2)。


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点在原点,焦点在
的顶点在原点,焦点在![]() 轴上,且抛物线上有一点
轴上,且抛物线上有一点![]() 到焦点的距离为5.
到焦点的距离为5.
(1)求该抛物线![]() 的方程;
的方程;
(2)已知抛物线上一点![]() ,过点
,过点![]() 作抛物线的两条弦
作抛物线的两条弦![]() 和
和![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
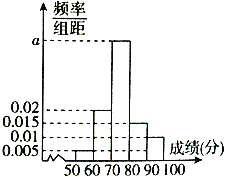
【题目】为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示.成绩落在[70,80)中的人数为20.
男生 | 女生 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
(Ⅰ)求a和n的值;
(Ⅱ)根据样本估计总体的思想,估计该校高二学生物理成绩的平均数![]() 和中位数m;
和中位数m;
(Ⅲ)成绩在80分以上(含80分)为优秀,样本中成绩落在[50,80)中的男、女生人数比为1:2,成绩落在[80,100]中的男、女生人数比为3:2,完成2×2列联表,并判断是否有95%的把握认为物理成绩优秀与性别有关.
参考公式和数据:K2=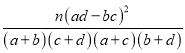 .
.
P(K2≥k) | 0.50 | 0.05 | 0.025 | 0.005 |
k | 0.455 | 3.841 | 5.024 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
商店名称 | A | B | C | D | E |
销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性.
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)所示,已知四边形![]() 是由直角△
是由直角△![]() 和直角梯形
和直角梯形![]() 拼接而成的,其中
拼接而成的,其中![]()
![]() .且点
.且点![]() 为线段
为线段![]() 的中点,
的中点, ![]() ,
, ![]() 现将△
现将△![]() 沿
沿![]() 进行翻折,使得二面角
进行翻折,使得二面角![]()
![]() 的大小为
的大小为![]() ,得到图形如图(2)所示,连接
,得到图形如图(2)所示,连接![]() ,点
,点![]() 分别在线段
分别在线段![]() 上.
上.


(1)证明: ![]() ;
;
(2)若三棱锥![]() 的体积为四棱锥
的体积为四棱锥![]() 体积的
体积的![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com