练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】我国古代数学名著《孙子算经》中有如下问题：“今有三女，长女五日一归，中女四日一归，少女三日一归．问：三女何日相会？” 意思是：“一家出嫁的三个女儿中，大女儿每五天回一次娘家，二女儿每四天回一次娘家，小女儿每三天回一次娘家．三个女儿从娘家同一天走后，至少再隔多少天三人再次相会？”假如回娘家当天均回夫家，若当地风俗正月初二都要回娘家，则从正月初三算起的一百天内，有女儿回娘家的天数有

    A. B. C. D.

    【答案】C

    【解析】小女儿、二女儿和大女儿回娘家的天数分别是33,25,20，小女儿和二女儿、小女儿和大女儿、二女儿和大女儿回娘家的天数分别是8,6,5，三个女儿同时回娘家的天数是1，所以有女儿在娘家的天数是：33+25+20-(8+6+5)+1=60．

    故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列命题：①在线性回归模型中，相关指数表示解释变量对于预报变量的贡献率， 越接近于1，表示回归效果越好；②两个变量相关性越强，则相关系数的绝对值就越接近于1；③在回归直线方程中，当解释变量每增加一个单位时，预报变量平均减少0.5个单位；④对分类变量与，它们的随机变量的观测值来说， 越小，“与有关系”的把握程度越大.其中正确命题的个数是（ ）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，a=7，b=8，cosB= –．

    （Ⅰ）求∠A；

    （Ⅱ）求AC边上的高．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=logm（m＞0且m≠1），

    （I）判断f（x）的奇偶性并证明；

    （II）若m=，判断f（x）在（3，+∞）的单调性（不用证明）；

    （III）若0＜m＜1，是否存在β＞α>0，使f（x）在[α，β]的值域为[logmm（β-1），logm（α-1）]？若存在，求出此时m的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正项数列满足4Sn=（an+1）2 ．
    （1）求数列{an}的通项公式；
    （2）设bn= ， 求数列{bn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC﹣A1B1C1中，AA1=AC=2AB=2，且BC1⊥A1C．
    （Ⅰ）求证：平面ABC1⊥平面A1C1CA；
    （Ⅱ）设D是A1C1的中点，判断并证明在线段BB1上是否存在点E，使DE∥平面ABC1；若存在，求三棱锥E﹣ABC1的体积．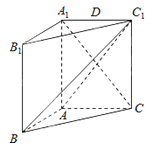

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】圆心在y轴上，半径为1，且过点（1，2）的圆的方程为（　　）
    A.x2+（y﹣2）2=1
    B.x2+（y+2）2=1
    C.（x﹣1）2+（y﹣3）2=1
    D.x2+（y﹣3）2=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列命题：①定义在上的函数满足，则一定不是上的减函数；

    ②用反证法证明命题“若实数，满足，则都为0”时，“假设命题的结论不成立”的叙述是“假设都不为0”；

    ③把函数的图象向右平移个单位长度，所得到的图象的函数解析式为；

    ④“”是“函数为奇函数”的充分不必要条件.

    其中所有正确命题的序号为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知矩阵A的逆矩阵A﹣1= ．
    （1）求矩阵A；
    （2）求矩阵A﹣1的特征值以及属于每个特征值的一个特征向量．

    查看答案和解析>>

    同步练习册答案