
【题目】(2015·江苏) 已知函数f(x)=x3+ax2+b(a,b![]() R).
R).
(1)试讨论f(x)的单调性;
(2)若b=c-a(实数c是a与无关的常数),当函数f(x)有三个不同的零点时,a的取值范围恰好是(-![]() ,-3)
,-3)![]() (1,
(1,![]() )
)![]() (
(![]() ,+
,+![]() ),求c的值.
),求c的值.
【答案】
(1)
当a=0时,f(x)在(-![]() , +
, +![]() )上单调递增, 当a>0时,f(x)在(-
)上单调递增, 当a>0时,f(x)在(-![]() , -
, -![]() ), (0,+
), (0,+![]() )上单调递增, 在(-
)上单调递增, 在(-![]() ,0)上单调递减,
,0)上单调递减,
当a<0时,f(x)在(-![]() , 0), (-
, 0), (-![]() ,+
,+![]() )上单调递增, 在(0, -
)上单调递增, 在(0, -![]() )上单调递减。
)上单调递减。
(2)
c=1.
【解析】(1) f'(x)=3x2+2ax, 令 f'(x)=0, 解得x1=0, x2=-![]() .
.
当a=0时,因为f'(x)=3x2>0,(x≠0), 所以 函数f(x)(-![]() , +
, +![]() )上单调递增,当a>0时,x
)上单调递增,当a>0时,x![]() (-
(-![]() ,-
,-![]() )
)![]() (0,+
(0,+![]() )时, f'(x)>0 , x
)时, f'(x)>0 , x![]() (-
(-![]() ,0), f'(x)<0 , 所以函数f(x)在(-
,0), f'(x)<0 , 所以函数f(x)在(-![]() , -
, -![]() ), (0,+
), (0,+![]() )上单调递增, 在(-
)上单调递增, 在(-![]() ,0)上单调递减。 当a<0时,x
,0)上单调递减。 当a<0时,x![]() (-
(-![]() ,0)
,0)![]() (-
(-![]() , +
, +![]() )时,f'(x)>0, x
)时,f'(x)>0, x![]() (0, -
(0, -![]() )时,f'(x)<0, 所以 f(x)在(-
)时,f'(x)<0, 所以 f(x)在(-![]() , 0), (-
, 0), (-![]() ,+
,+![]() )上单调递增, 在(0, -
)上单调递增, 在(0, -![]() )上单调递减。
)上单调递减。
(2)由(1)知, 函数f(x)的两个极值为f(0)=b, f(-![]() )=
)=![]() a3+b,则函数f(x)有三个零点等价于f(0)·f(-
a3+b,则函数f(x)有三个零点等价于f(0)·f(-![]() )=b(
)=b(![]() a3+b)<0, 从而
a3+b)<0, 从而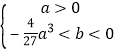 或
或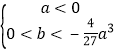 , 又b=c-a,所以当a>0时,
, 又b=c-a,所以当a>0时,![]() a3-a+c>0或当a<0时,
a3-a+c>0或当a<0时, ![]() a3-a+c<0.
a3-a+c<0.
设g(a)=![]() a3-a+c,因为函数f(x)有三个零点时, a的取值范围恰好是(-
a3-a+c,因为函数f(x)有三个零点时, a的取值范围恰好是(-![]() ,-3)
,-3)![]() (1,
(1,![]() )
)![]() (
(![]() ,+
,+![]() ), 则(-
), 则(-![]() ,-3)上g(a)<0,且在(1,
,-3)上g(a)<0,且在(1,![]() )
)![]() (
(![]() ,+
,+![]() )上g(a)>0均恒成立, 从而g(-3)=c-1≤0,且g(
)上g(a)>0均恒成立, 从而g(-3)=c-1≤0,且g(![]() )=c-1≥0, 因此c=1.
)=c-1≥0, 因此c=1.
此时, f(x)=x3+ax2+1-a=(x+1)[x2+(a-1)x+1-a], 因函数有三个零点, 则x2+(a-1)x+1-a有两个异于-1的不等实根, 所以△=(a-1)2-4(1-a)=a2+2a-3>0, 且(-1)2-(a-1)+1-1≠0,解得a![]() (-
(-![]() ,-3)
,-3)![]() (1,
(1,![]() )
)![]() (
(![]() ,+
,+![]() ). 综上c=1.
). 综上c=1.
【考点精析】利用函数的单调性和函数的零点对题目进行判断即可得到答案,需要熟知注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】![]() 如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记
如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记![]() BOP=x,将动P到A、B两点距离之和表示为x的函数f(x),则y=f(x)的图像大致为()
BOP=x,将动P到A、B两点距离之和表示为x的函数f(x),则y=f(x)的图像大致为()
A.
B.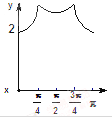
C.
D.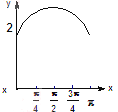
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点。设异面直线EM与AF所成的角为![]() ,则cos
,则cos![]() 的最大值为 .
的最大值为 .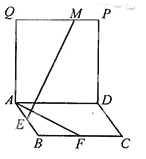
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点。
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线AC1与平面AA1BB1所成的角为45°,求三棱锥F-AEC的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
(Ⅰ)求证:BE//平面ADE ;
(Ⅱ)求平面AEF与平面BEC所成锐二面角的余弦值.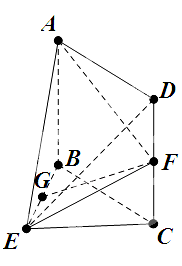
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
如图,在阳马P-ABCD中,侧棱![]() 底面
底面![]() ,且
,且![]() ,过棱
,过棱![]() 的中点
的中点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]()
(1)证明:![]() 平面
平面![]() .试判断四面体
.试判断四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写
是否为鳖臑,若是,写出其每个面的直角(只需写
出结论);若不是,说明理由;
(2)若面![]() 与面
与面![]() 所成二面角的大小为
所成二面角的大小为![]() , 求
, 求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com