
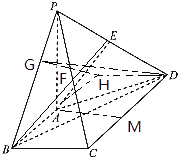
【题目】如图,四棱锥P﹣ABCD的底面是直角梯形,∠ABC=∠BCD= ![]() ,AB=BC=1,CD=2,PA⊥平面ABCD,E是PD的中点.
,AB=BC=1,CD=2,PA⊥平面ABCD,E是PD的中点. 
(1)求证:AE∥平面PBC;
(2)若直线AE与直线BC所成角等于 ![]() ,求二面角D﹣PB﹣A平面角的余弦值.
,求二面角D﹣PB﹣A平面角的余弦值.
【答案】
(1)证明:取PC中点F,连结EF、BF,
∴△PCD中,EF ![]()
![]() ,AB
,AB ![]()
![]() ,
,
∴EF ![]() AB,
AB,
∴四边形ABFE为平行四边形,
∵AE∥BF,AE平面PBC,BF平面PBC,
∴AE∥平面PBC.
(2)解:AE与直线BC所成角为 ![]() ,
, ![]() ,
,
∴BP= ![]() ,∴PA=
,∴PA= ![]() ,
,
延长BA一倍到H,连结DH,再作HG⊥BP,连结DG,
则∠DGH是二面角D﹣PB﹣A的平面角,
DH=1,FG× ![]() ,HG=
,HG= ![]() ,
,
∴tan∠DGH= ![]() ,
,
∴cos∠DGH= ![]()
![]() .
.
∴二面角D﹣PB﹣A平面角的余弦值为 ![]() .
.
【解析】(1)取PC中点F,连结EF、BF,推导出四边形ABFE为平行四边形,从而AE∥BF,由此能证明AE∥平面PBC.(2)AE与直线BC所成角为 ![]() ,延长BA一倍到H,连结DH,再作HG⊥BP,连结DG,∠DGH是二面角D﹣PB﹣A的平面角,由此能求出二面角D﹣PB﹣A平面角的余弦值.
,延长BA一倍到H,连结DH,再作HG⊥BP,连结DG,∠DGH是二面角D﹣PB﹣A的平面角,由此能求出二面角D﹣PB﹣A平面角的余弦值.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆的方程;
(2)若过点![]() 且斜率为k的直线l与椭圆相交于不同的两点A,B,试问在x轴上是否存在点
且斜率为k的直线l与椭圆相交于不同的两点A,B,试问在x轴上是否存在点![]() ,使
,使![]() 是与
是与![]() 无关的常数?若存在,求出点
无关的常数?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:

(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x=3是函数f(x)=aln(1+x)+x2﹣10x的一个极值点.
(Ⅰ)求a;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)若直线y=b与函数y=f(x)的图象有3个交点,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+y2=r2(r>0)与直线l:y=x+3,且直线l有唯一的一个点P,使得过P点作圆C的两条切线互相垂直,则r=;设EF是直线l上的一条线段,若对于圆C上的任意一点Q,∠EQF≥ ![]() ,则|EF|的最小值= .
,则|EF|的最小值= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,角A、B、C所对的边分别为a、b、c,且2acosB=3b﹣2bcosA. 
(1)求 ![]() 的值;
的值;
(2)设AB的中垂线交BC于D,若cos∠ADC= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,若关于x的方程f2(x)﹣bf(x)+c=0(b,c∈R)有8个不同的实数根,则b+c的取值范围为( )
,若关于x的方程f2(x)﹣bf(x)+c=0(b,c∈R)有8个不同的实数根,则b+c的取值范围为( )
A.(﹣∞,3)
B.(0,3]
C.[0,3]
D.(0,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com