
分析 (Ⅰ)先求导,根据导数求出函数的最值,问题即可解决,
(Ⅱ)欲证明不等式$\frac{{f(x)-f({x_1})}}{{x-{x_1}}}<\frac{{f(x)-f({x_2})}}{{x-{x_2}}}$成立,从图象分析可先证$\frac{f(x)-f({x}_{1})}{x-{x}_{1}}$<f′(x)<$\frac{f(x)-f({x}_{2})}{x-{x}_{2}}$,分别构造函数,根据导数和函数的单调性和最值关系即可证明
解答 解:(Ⅰ)f(x)=xlnx+a的定义域为(0,+∞),
∴f′(x)=1+lnx,
令f′(x)=0,解得x=$\frac{1}{e}$,
当f′(x)>0时,即x>$\frac{1}{e}$时,函数f(x)单调递增,
当f′(x)<0时,即0<x<$\frac{1}{e}$时,函数f(x)单调递减,
∴f(x)min=f($\frac{1}{e}$)=-$\frac{1}{e}$+a,
∵f(x)≥0恒成立,
∴-$\frac{1}{e}$+a≥0,
∴a≥$\frac{1}{e}$,
(Ⅱ)证明:由(Ⅰ)知,f′(x)=1+lnx,
∴f′(x)在(0,+∞)上为增函数,
欲证明不等式$\frac{{f(x)-f({x_1})}}{{x-{x_1}}}<\frac{{f(x)-f({x_2})}}{{x-{x_2}}}$成立,
从图象分析可先证$\frac{f(x)-f({x}_{1})}{x-{x}_{1}}$<f′(x)<$\frac{f(x)-f({x}_{2})}{x-{x}_{2}}$,
先证明$\frac{f(x)-f({x}_{1})}{x-{x}_{1}}$<f′(x)=lnx+1,0<x1<x,
即证f(x)-f(x1)-(x-x1)(lnx+1)<0,
设F(x)=f(x)-f(x1)-(x-x1)(lnx+1),0<x1<x<x2,
∴F′(x)=f′(x)-(lnx+1)-$\frac{x-{x}_{1}}{x}$=(lnx+1)-(lnx+1)-(1-$\frac{{x}_{1}}{x}$)=$\frac{{x}_{1}}{x}$-1<0,
∴F(x)在(x1,x2)内为减函数,
∴F(x)<F(x1)=0,
∴$\frac{f(x)-f({x}_{1})}{x-{x}_{1}}$<lnx+1对于(x1,x2)成立,
欲证lnx+1<$\frac{f(x)-f({x}_{2})}{x-{x}_{2}}$,即证f(x)-f(x2)-(x-x2)(lnx+1)<0,
设G(x)=f(x)-f(x2)-(x-x2)(lnx+1),0<x1<x<x2,
∴G′(x)=f′(x)-(lnx+1)-$\frac{x-{x}_{2}}{x}$=(lnx+1)-(lnx+1)-(1-$\frac{{x}_{2}}{x}$)=$\frac{{x}_{2}}{x}$-1>0,
∴G(x)在(x1,x2)内为增函数,
∴G(x)<G(x2)=0,
∴lnx+1<$\frac{f(x)-f({x}_{2})}{x-{x}_{2}}$对于(x1,x2)成立,
综上所述对于任意x∈(x1,x2),不等式$\frac{{f(x)-f({x_1})}}{{x-{x_1}}}<\frac{{f(x)-f({x_2})}}{{x-{x_2}}}$成立
点评 本题考查了函数恒成立的问题,以及导数和函数的单调性和最值得关系,考查了学生的运算能力和转化能力,属于难题


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
| A. | ±cos40° | B. | cos40° | C. | -cos40° | D. | ±|cos40°| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
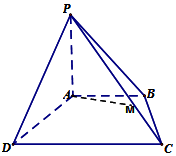 四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=$\frac{1}{2}$CD,AB∥CD,∠ADC=90°.
四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=$\frac{1}{2}$CD,AB∥CD,∠ADC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{15}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | b>a>c | C. | a>b>c | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2016}{2017}$ | B. | $\frac{2017}{2016}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{2018}{2017}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com