已知f(x)为R上的偶函数,当x≥0时,f(x)=ln(x+2).
(Ⅰ)当x<0时,求f(x)的解析式;
(Ⅱ)当m∈R时,试比较f(m-1)与f(3-m)的大小;
(Ⅲ)求最小的整数m(m≥-2),使得存在实数t,对任意的x∈[m,10],都有f(x+t)≤2ln|x+3|.
【答案】
分析:(Ⅰ)当x<0时,-x>0,利用f(x)为R上的偶函数,当x≥0时,f(x)=ln(x+2),可求函数的解析式;
(Ⅱ)当x≥0时,f(x)=ln(x+2)单调递增,而f(x)是偶函数,所以f(x)在(-∞,0)上单调递减,从而可得当m>2时,f(m-1)>f(3-m);当m=2时,f(m-1)=f(3-m);当m<2时,f(m-1)<f(3-m);
(Ⅲ)当x∈R时,f(x)=ln(|x|+2),则|x+t|+2≤(x+3)
2对x∈[m,10]恒成立,从而有

对x∈[m,10]恒成立,由此可求适合题意的最小整数m的值.
解答:解:(Ⅰ)当x<0时,-x>0,
∵f(x)为R上的偶函数,当x≥0时,f(x)=ln(x+2)
∴f(x)=f(-x)=ln(-x+2)…(3分)
(Ⅱ)当x≥0时,f(x)=ln(x+2)单调递增,而f(x)是偶函数,所以f(x)在(-∞,0)上单调递减,
所以f(m-1)>f(3-m)
所以|m-1|>|3-m|
所以(m-1)
2>(3-m)
2
所以m>2…(6分)
所以当m>2时,f(m-1)>f(3-m);当m=2时,f(m-1)=f(3-m);当m<2时,f(m-1)<f(3-m)…(8分)
(Ⅲ)当x∈R时,f(x)=ln(|x|+2),则由f(x+t)≤2ln|x+3|,得ln(|x+t|+2)≤ln(x+3)
2,
即|x+t|+2≤(x+3)
2对x∈[m,10]恒成立…(12分)
从而有

对x∈[m,10]恒成立,因为m≥-2,
所以
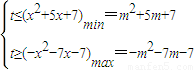
…(14分)
因为存在这样的t,所以-m
2-7m-7≤m
2+5m+7,即m
2+6m+7≥0…(15分)
又m≥-2,所以适合题意的最小整数m=-1…(16分)
点评:本题考查函数单调性与奇偶性的综合,考查函数的解析式,考查恒成立问题,分离参数,确定函数的最值是关键.

 对x∈[m,10]恒成立,由此可求适合题意的最小整数m的值.
对x∈[m,10]恒成立,由此可求适合题意的最小整数m的值. 对x∈[m,10]恒成立,因为m≥-2,
对x∈[m,10]恒成立,因为m≥-2,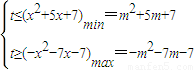 …(14分)
…(14分)
