
【题目】袋中装有6个球,红蓝两色各半,从袋中不放回取球![]() 次,每次取1个球.
次,每次取1个球.
(1)求下列事件的概率:
①事件![]() :
:![]() ,取出的球同色;
,取出的球同色;
②事件![]() :
:![]() ,第
,第![]() 次恰好将红球全部取出;
次恰好将红球全部取出;
(2)若第![]() 次恰好取到第一个红球,求抽取次数
次恰好取到第一个红球,求抽取次数![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)①![]() ;②
;②![]() ;(2)分布列见解析,
;(2)分布列见解析,![]() .
.
【解析】
(1)①![]() ,基本事件总数n=
,基本事件总数n=![]() =15, 取出的球同色包含的基本事件个数m=2
=15, 取出的球同色包含的基本事件个数m=2![]() =6,由古典概型概率计算公式即可求得答案;
=6,由古典概型概率计算公式即可求得答案;
②![]() ,基本事件总数n=
,基本事件总数n=![]() ,第k次恰好将红球全部取出包含的基本事件个数m=
,第k次恰好将红球全部取出包含的基本事件个数m=![]() ,由古典概型概率计算公式即可求得答案;
,由古典概型概率计算公式即可求得答案;
(2)![]() 的可能取值为1,2,3,4,分别计算概率并列出分布列,再由数学期望计算公式即可求得答案.
的可能取值为1,2,3,4,分别计算概率并列出分布列,再由数学期望计算公式即可求得答案.
(1)袋中装有6个球,红蓝两色各半,从袋中不放回取球k (1≤k≤6, k∈Z)次,每次取1个球.
①k=2,基本事件总数n=![]() =15,
=15,
事件A:k=2,取出的球同色包含的基本事件个数m=2![]() =6,
=6,
所以事件A的概率![]()
②k=5,基本事件总数n=![]()
事件B:k=5,第k次恰好将红球全部取出包含的基本事件个数m=![]()
所以事件B的概率![]()
(2)![]() 的可能取值为1,2,3,4
的可能取值为1,2,3,4
![]() ,
,
![]()
![]()
![]()
∴![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 |
|
|
|
|
|
∴![]()


科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是菱形,AC=BC=2,∠CBB1=![]() ,点A在平面BCC1B1上的投影为棱BB1的中点E.
,点A在平面BCC1B1上的投影为棱BB1的中点E.
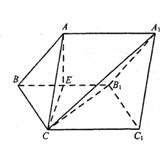
(1)求证:四边形ACC1A1为矩形;
(2)求二面角E-B1C-A1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
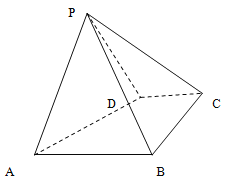
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,侧面
,侧面![]() 底面
底面![]() ,且
,且![]() 是以
是以![]() 为底的等腰三角形.
为底的等腰三角形.
(Ⅰ)证明:![]()
(Ⅱ)若四棱锥![]() 的体积等于
的体积等于![]() .问:是否存在过点
.问:是否存在过点![]() 的平面
的平面![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点
的中心在原点![]() ,焦点在
,焦点在![]() 轴上,左右焦点分别为
轴上,左右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,右焦点到右顶点的距离为1.
,右焦点到右顶点的距离为1.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,则
,则![]() 的面积是否存在最大值?若存在,求出这个最大值及直线
的面积是否存在最大值?若存在,求出这个最大值及直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)分别求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,交曲线
两点,交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
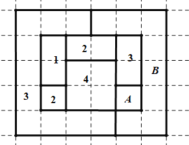
【题目】如图,网格纸上小正方形的边长为1,粗实线围成的各区域上分别且只能标记数字1,2,3,4,相邻区域标记的数字不同,其中,区域![]() 和区域
和区域![]() 标记的数字丢失.若在图上随机取一点,则该点恰好取自标记为1的区域的概率所有可能值中,最大的是( )
标记的数字丢失.若在图上随机取一点,则该点恰好取自标记为1的区域的概率所有可能值中,最大的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com