练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知0＜a＜
    π
    2
    ，sinα=
    4
    5

    （1）求
    sin2α+sin2α
    cos2α+cos2α
    的值；
    （2）求tan（α-
    5π
    4
    ）的值．
    分析：（1）利用平方关系和倍角公式即可得出；
    （2）利用商数关系和两角差的正切公式即可得出．
    解答：解：（1）∵0＜a＜
    π
    2
    ，sinα=
    4
    5
    ，∴cosα=
    		1-sin2α
    =
    3
    5
    ．
    ∴
    sin2α+sin2α
    cos2α+cos2α
    =
    sin2α+2sinαcosα
    cos2α+2cos2α-1
    =
    (
    4
    5
    )2+2×
    4
    5
    ×
    3
    5
    3×(
    3
    5
    )2-1
    =20；
    （2）由（1）可知：tanα=
    sinα
    cosα
    =
    4
    3
    ．
    ∴tan（α-
    5π
    4
    ）=tan(α-
    π
    4
    )    =
    tanα-tan
    π
    4
    1+tanαα•tan
    π
    4
    =
    4
    3
    -1
    1+
    4
    3
    ×1
    =
    1
    7
    ．
    点评：熟练掌握平方关系和倍角公式、商数关系和两角差的正切公式是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知两定点A（-2，0），B（1，0），动点P（x，y）满足|PA|=2|PB|．
    （1）求动点P的轨迹C的方程；
    （2）求
    y
    x+2
    的取值范围；
    （3）设点S在过点A且垂直于x轴的直线l上运动，作SM，SN与轨迹C相切（M，N为切点）．
    ①求证：M，B，N三点共线；
    ②求
    SM
    •
    SN
    的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知三点A（-2-a,0）,P(-2-a,t),F(a,0),其中a为大于零的常数，t为变数，平面内动点M满足·=0，且||=||+2.

    （1）求动点M的轨迹;

    （2）若动点M的轨迹在x轴上方的部分与圆心在C(a+4,0),半径为4的圆相交于两点S、T，求证：C落在以S、T为焦点过F的椭圆上.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知两定点A（-2，0），B（1，0），动点P（x，y）满足|PA|=2|PB|．
    （1）求动点P的轨迹C的方程；
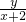    （2）求数学公式的取值范围；
    （3）设点S在过点A且垂直于x轴的直线l上运动，作SM，SN与轨迹C相切（M，N为切点）．
    ①求证：M，B，N三点共线；
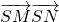    ②求数学公式的最小值．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知两定点A（-2，0），B（1，0），动点P（x，y）满足|PA|=2|PB|．
    （1）求动点P的轨迹C的方程；
    （2）求
    y
    x+2
    的取值范围；
    （3）设点S在过点A且垂直于x轴的直线l上运动，作SM，SN与轨迹C相切（M，N为切点）．
    ①求证：M，B，N三点共线；
    ②求
    SM
    •
    SN
    的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知0<a<1,在函数y= logax  (x≥1)的图象上有A、B、C三点，它们的横坐标分别是t、t+2、t+4；

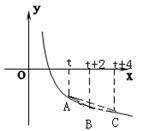    ①、记△ABC的面积为S，求出S=f(t)的表达式；并判断出S== f(t)的单调性；

    ②、求出S=f(t)的最大值。

    查看答案和解析>>

    同步练习册答案