
【题目】(本小题满分14分)已知递增等差数列![]() 中的
中的![]() 是函数
是函数![]() 的两个零点.数列
的两个零点.数列![]() 满足,点
满足,点![]() 在直线
在直线![]() 上,其中
上,其中![]() 是数列
是数列![]() 的前
的前![]() 项和.
项和.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:本题主要考查函数零点、等差数列的通项公式、等比数列的通项公式、等比数列的前n项和公式、错位相减法等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力. 第一问,先解出函数![]() 的两个零点,由于数列
的两个零点,由于数列![]() 是递增数列,排除一组解,再利用等差数列的通项公式求
是递增数列,排除一组解,再利用等差数列的通项公式求![]() ,利用点在直线上,得到
,利用点在直线上,得到![]() 与
与![]() 的关系式,再利用
的关系式,再利用![]() 证出数列
证出数列![]() 是等比数列,最后利用等比数列的前n项和公式求
是等比数列,最后利用等比数列的前n项和公式求![]() ;第二问,利用第一问的结论,先求出
;第二问,利用第一问的结论,先求出![]() 表达式,利用错位相减法求和,在此过程中要用到等比数列的前n项和公式计算.
表达式,利用错位相减法求和,在此过程中要用到等比数列的前n项和公式计算.
试题解析:(1)∵![]() ,
,![]() 是函数
是函数![]() 的两个零点,则
的两个零点,则
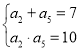 ,解得:
,解得: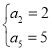 或
或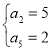 . ..2分
. ..2分
又等差数列![]() 递增,则
递增,则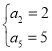 ,∴
,∴![]() .4分
.4分
∵点![]() 在直线
在直线![]() 上,则
上,则![]() 。
。
当![]() 时,
时,![]() ,即
,即![]() . .5分
. .5分
当![]() 时,
时, ![]() ,即
,即![]() . .. 6分
. .. 6分
∴数列![]() 为首项为
为首项为![]() ,公比为
,公比为![]() 的等比数列,即
的等比数列,即![]() . . 7分
. . 7分
(2)由(1)知:![]() 且
且![]() , ... 8分
, ... 8分
则![]() ...9分
...9分
∴![]() ①
①
![]() ② . 10分
② . 10分
①-②得:![]() . 12分
. 12分
∴![]() . 或写
. 或写 ![]() . 14分
. 14分


科目:高中数学 来源: 题型:
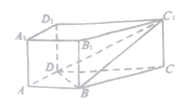
【题目】如图,四棱柱![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ,若存在,请确定点
,若存在,请确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节油降耗技术发行后生产甲产品过程中记录的产量 x (吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出 y 关于 x 的线性回归方程![]()
(3)已知该厂技改前 100 吨甲产品的生产能耗为 90 吨标准煤,试根据(2)求出的线性回归方程,预测生产100 吨甲产品的生产能耗比技改前降低多少吨标准煤?(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求a的取值范围
(3)若x∈[t,t+2],试求y=f(x)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=lg ![]() (x≠0,x∈R)有下列命题:
(x≠0,x∈R)有下列命题:
①函数y=f(x)的图象关于y轴对称;
②在区间(﹣∞,0)上,函数y=f(x)是减函数;
③函数f(x)的最小值为lg2;
④在区间(1,+∞)上,函数f(x)是增函数.
其中正确命题序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]()
(1)若不等式![]() 对
对![]() 恒成立,求
恒成立,求![]() 的值;
的值;
(2)若![]() 在
在![]() 内有两个极值点,求负数
内有两个极值点,求负数![]() 的取值范围;
的取值范围;
(3)已知 ,若对任意实数
,若对任意实数![]() ,总存在实数
,总存在实数![]() ,使得
,使得![]() 成立,求正实数
成立,求正实数![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为偶函数.
为偶函数.
(1)求实数![]() 的值;
的值;
(2)记集合![]() ,
, ![]() ,
, ![]() ,判断
,判断![]() 与
与![]() 的关系;
的关系;
(3)当![]() (m>0,n>0)时,若函数f(x)的值域为[2-3m,2-3n],求m,n的值.
(m>0,n>0)时,若函数f(x)的值域为[2-3m,2-3n],求m,n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设G为△ABC的重心,过G作直线l分别交线段AB,AC(不与端点重合)于P,Q.若 ![]() =λ
=λ ![]() ,
, ![]() =μ
=μ ![]() .
. 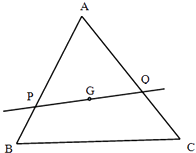
(1)求 ![]() 的值;
的值;
(2)求λμ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数{an}:a1=t,n2Sn+1=n2(Sn+an)+an2 , n=1,2,….
(1)设{an}为等差数列,且前两项和S2=3,求t的值;
(2)若t= ![]() ,证明:
,证明: ![]() ≤an<1.
≤an<1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com