
为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:

(Ⅰ)若用表中数据所得频率代替概率,则处罚10元时与处罚20元时,行人会闯红灯的概率的差是多少?
(Ⅱ)若从这5种处罚金额中随机抽取2种不同的金额进行处罚,在两个路口进行试验.
①求这两种金额之和不低于20元的概率;
②若用X表示这两种金额之和,求X的分布列和数学期望.
(1)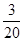
(2)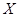 的可能取值为5,10,15,20,25,30,35,分布列为
的可能取值为5,10,15,20,25,30,35,分布列为
|
|
5 |
10 |
15 |
20 |
25 |
30 |
35 |
|
|
|
|
|
|
|
|
|
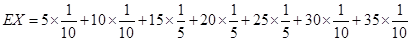 =20
=20
【解析】
试题分析:解:(Ⅰ)由条件可知,处罚10元会闯红灯的概率与处罚20元会闯红灯的概率的差是: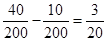 . (4分)
. (4分)
(Ⅱ)①设“两种金额之和不低于20元”的事件为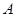 ,从5种金额中随机抽取2种,总的抽选方法共有
,从5种金额中随机抽取2种,总的抽选方法共有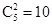 种,满足金额之和不低于20元的有6种,
种,满足金额之和不低于20元的有6种,
故所求概率为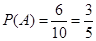 . (8分)
. (8分)
②根据条件,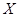 的可能取值为5,10,15,20,25,30,35,分布列为
的可能取值为5,10,15,20,25,30,35,分布列为
|
|
5 |
10 |
15 |
20 |
25 |
30 |
35 |
|
|
|
|
|
|
|
|
|
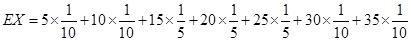 =20. (12分)
=20. (12分)
考点:古典概型和分布列
点评:主要是考查了古典概型的概率公式,以及分布列和数学期望值的求解,属于中档题。


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
| 处罚金额x(元) | 0 | 5 | 10 | 15 | 20 |
| 会闯红灯的人数y | 80 | 50 | 40 | 20 | 10 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省十所名校高三第三次联考理科数学试卷(解析版) 题型:解答题
为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:

(Ⅰ)若用表中数据所得频率代替概率,则处罚10元时与处罚20元时,行人会闯红灯的概率的差是多少?
(Ⅱ)若从这5种处罚金额中随机抽取2种不同的金额进行处罚,在两个路口进行试验.
求这两种金额之和不低于20元的概率;
②若用X表示这两种金额之和,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2014届甘肃省高二下学期期末考试理科数学试卷(解析版) 题型:解答题
为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:
|
处罚金额x(元) |
0 |
5 |
10 |
15 |
20 |
|
会闯红灯的人数y |
80 |
50 |
40 |
20 |
10 |
若用表中数据所得频率代替概率.现从这5种处罚金额中随机抽取2种不同的金额进行处罚,在两个路口进行试验.
(Ⅰ)求这两种金额之和不低于20元的概率;
(Ⅱ)若用X表示这两种金额之和,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省兰州一中高二(下)期末数学试卷(理科)(解析版) 题型:解答题
| 处罚金额x(元) | 5 | 10 | 15 | 20 | |
| 会闯红灯的人数y | 80 | 50 | 40 | 20 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com