
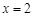 处取到,比较大小知f(x)在区间[1,2]上的最大值为f(2)=1,即为往年的收益,所以商户甲采取降低单价,提高销量的营销策略不能获得比往年更大的收益.
处取到,比较大小知f(x)在区间[1,2]上的最大值为f(2)=1,即为往年的收益,所以商户甲采取降低单价,提高销量的营销策略不能获得比往年更大的收益.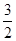 ,或x=
,或x=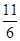 .列表如下:
.列表如下:| x | (1,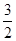 ) ) | 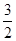 | (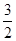 , ,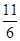 ) ) | 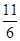 | (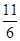 ,2) ,2) |
| f ′(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
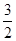 )=1,f(2)=1,所以f(x)在区间[1,2]上的最大值为1(万元).
)=1,f(2)=1,所以f(x)在区间[1,2]上的最大值为1(万元).

科目:高中数学 来源:不详 题型:解答题
 ax2-(2a+1)x+2lnx(a∈R).
ax2-(2a+1)x+2lnx(a∈R).查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
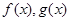 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当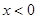 时
时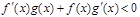 且
且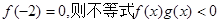 的解集为( )
的解集为( )| A.(-2,0)∪(2,+∞) |
| B.(-2,0)∪(0,2) |
| C.(-∞,-2)∪(2,+∞) |
| D.(-∞,-2)∪(0,2) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com