
【题目】已知数列![]() 是以
是以![]() 为公差的等差数列,数列
为公差的等差数列,数列![]() 是以
是以![]() 为公比的等比数列.
为公比的等比数列.
(1)若数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() ,求整数
,求整数![]() 的值;
的值;
(2)若![]() ,
,![]() ,
,![]() ,试问数列
,试问数列![]() 中是否存在一项
中是否存在一项![]() ,使得
,使得![]() 恰好可以表示为该数列中连续
恰好可以表示为该数列中连续![]() 项的和?请说明理由;
项的和?请说明理由;
(3)若![]() ,
,![]() ,
,![]() (其中
(其中![]() ,且
,且![]() 是
是![]() 的约数),求证:数列
的约数),求证:数列![]() 中每一项都是数列
中每一项都是数列![]() 中的项.
中的项.
【答案】(1)![]() ;(2)不存在,理由见解析;(3)证明见解析.
;(2)不存在,理由见解析;(3)证明见解析.
【解析】
(1)由等差等比数列的表达式an=2n,bn=2qn-1,代入S3<a1003+5b2-2010直接求解即得到答案.
(2)可以先假设数列{bn}中存在一项bk,满足bk=bm+bm+1+bm+2++bm+p-1,再根据已知的条件去验证,看是否能找出矛盾.如果没有矛盾即存在,否则这样的项bk不存在;
(3)由已知条件b1=ar,得b2=b1q=arq=as=ar+(s-r)d,结合等差等比数列的性质,可证数列![]() 中每一项是否都是数列
中每一项是否都是数列![]() 中的项.
中的项.
(1)由题意知,an=2n,bn=2qn-1,
∴由S3<a1003+5b2-2010,
可得到b1+b2+b3<a1003+5b2-2010b1-4b2+b3<2006-2010q2-4q+3<0.
解得1<q<3,
又q为整数,
∴q=2
(2)假设数列{bn}中存在一项bk,满足bk=bm+bm+1+bm+2+…+bm+p-1,
∵bn=2n,
∴bk>bm+p-12k>2m+p-1k>m+p-1k≥m+p①
又
=2m+p-2m<2m+p,
∴k<m+p,此与①式矛盾.
∴这样的项bk不存在;
(3)由b1=ar,得b2=b1q=arq=as=ar+(s-r)d,
则![]()
又![]() ,
,
从而![]() ,
,
∵as≠arb1≠b2,
∴q≠1,又ar≠0,
故![]() .
.
又t>s>r,且(s-r)是(t-r)的约数,
∵q是整数,且q≥2,
对于数列中任一项bi(这里只要讨论i>3的情形),
有bi=arqi-1=ar+ar(qi-1-1)
=ar+ar(q-1)(1+q+q2+…+qi-2)
=ar+d(s-r)(1+q+q2+…+qi-2)
=ar+[((s-r)(1+q+q2+…+qi-2)+1)-1]d,
由于(s-r)(1+q+q2+…+qi-2)+1是正整数,
∴bi一定是数列的项.
故得证.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() 满足:①对任意
满足:①对任意![]() ,存在正常数
,存在正常数![]() ,都有
,都有![]() 成立;②
成立;②![]() 的值域为
的值域为![]() (
(![]() ),则函数
),则函数![]() 是( )
是( )
A.周期为2的周期函数B.周期为4的周期函数
C.奇函数D.偶函数
查看答案和解析>>
科目:高中数学 来源: 题型:
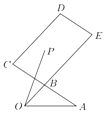
【题目】如图,B是AC的中点,![]() ,P是平行四边形BCDE内(含边界)的一点,且
,P是平行四边形BCDE内(含边界)的一点,且![]() .有以下结论:
.有以下结论:
①当x=0时,y∈[2,3];
②当P是线段CE的中点时,![]() ;
;
③若x+y为定值1,则在平面直角坐标系中,点P的轨迹是一条线段;
④x﹣y的最大值为﹣1;
其中你认为正确的所有结论的序号为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某环线地铁按内、外环线同时运行,内、外环线的长均为30千米(忽略内、外环线长度差异).
(1)当9列列车同时在内环线上运行时,要使内环线乘客最长候车时间为10分钟,求内环线列车的最小平均速度;
(2)新调整的方案要求内环线列车平均速度为25千米/小时,外环线列车平均速度为30千米/小时.现内、外环线共有18列列车全部投入运行,要使内外环线乘客的最长候车时间之差不超过1分钟,向内、外环线应各投入几列列车运行?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人的月工资由基础工资和绩效工资组成2010年每月的基础工资为2100元、绩效工资为2000元从2011年起每月基础工资比上一年增加210元、绩效工资为上一年的![]() 照此推算,此人2019年的年薪为______万元(结果精确到
照此推算,此人2019年的年薪为______万元(结果精确到![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在△AOB中,∠AOB=90°,AO=2,OB=1,△AOC可以通过△AOB以直线AO为轴旋转得到,且OB⊥OC,点D为斜边AB的中点.
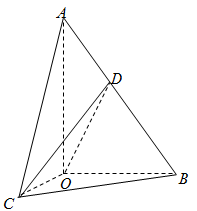
(1)求异面直线OB与CD所成角的余弦值;
(2)求直线OB与平面COD所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com