
【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),
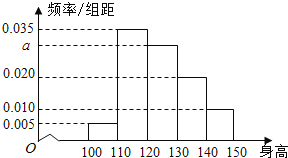
(1)由图中数据求a的值;
(2)若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为多少?
(3)估计这所小学的小学生身高的众数,中位数(保留两位小数)及平均数.
【答案】(1)a=0.030;(2)3人;(3)众数115cm,中位数123.33cm,平均数124.5cm
【解析】
(1)根据频率和为1,求出[120,130)频率,再除以10,即为所求的值;
(2)先求出三组的人数,根据分层抽样按比例分配,将18人按比例分配,即可求解;
(3)根据直方图,频率最大组的中间值,为众数;从左到右求出频率和为0.5所在的组,再求出在该组所占的比例,即可求出中位数;根据平均数的公式,即可求解.
(1)因为直方图中的各个矩形的面积之和为1,
所以有10×(0.005+0.035+a+0.020+0.010)=1,
解得a=0.030;
(2)由直方图知,三个区域内的学生总数为
100×10×(0.030+0.020+0.010)=60人,
其中身高在[140,150]内的学生人数为10人,
所以从身高在[140,150]范围内抽取的学生人数为
![]() 10=3人;
10=3人;
(3)根据频率分布直方图知,身高在[110,120)内的小矩形图最高,
所以该组数据的众数为![]() 115cm;
115cm;
又0.005×10+0.035×10=0.4<0.5,
0.4+0.030×10=0.7>0.5,
所以中位数在[120,130)内,
则中位数为![]() ;
;
根据频率分布直方图,计算平均数为
105×0.05+115×0.35+125×0.3+135×0.2+145×0.1=124.5cm.


 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】若方程![]() 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:
①若C为椭圆,则![]() ;
;
②若C为双曲线,则![]() 或
或![]() ;
;
③曲线C不可能是圆;
④若![]() ,曲线C为椭圆,且焦点坐标为
,曲线C为椭圆,且焦点坐标为![]() ;
;
⑤若![]() ,曲线C为双曲线,且虚半轴长为
,曲线C为双曲线,且虚半轴长为![]() .
.
其中真命题的序号为____________.(把所有正确命题的序号都填在横线上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,
,![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(2)设数列![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证:![]() ;
;
(3)当![]() 时,设函数
时,设函数![]() 的图象
的图象![]() 与函数
与函数![]() 的图象
的图象![]() 交于点
交于点![]() ,
,![]() ,过线段
,过线段![]() 的中点
的中点![]() 作
作![]() 轴的垂线分别交
轴的垂线分别交![]() ,
,![]() 于点
于点![]() ,问是否存在点
,问是否存在点![]() ,使
,使![]() 在
在![]() 处的切线与
处的切线与![]() 在
在![]() 处的切线平行?若存在,求出
处的切线平行?若存在,求出![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部门在上班高峰时段对甲、乙两座地铁站各随机抽取了50名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,单位:分钟)将统计数据按![]() ,
,![]() ,
,![]() ,…,
,…,![]() 分组,制成频率分布直方图如图所示:
分组,制成频率分布直方图如图所示:


(1)求a的值;
(2)记A表示事件“在上班高峰时段某乘客在甲站乘车等待时间少于20分钟”试估计A的概率;
(3)假设同组中的每个数据用该组区间左端点值来估计,记在上班高峰时段甲、乙两站各抽取的50名乘客乘车的平均等待时间分别为![]() ,求
,求![]() 的值,并直接写出
的值,并直接写出![]() 与
与![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() (
(![]() =1,2,…,6),如表所示:
=1,2,…,6),如表所示:
试销单价 | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量 | q | 84 | 83 | 80 | 75 | 68 |
已知![]() .
.
(Ⅰ)求出![]() 的值;
的值;
(Ⅱ)已知变量![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;
;
(参考公式:线性回归方程中![]() ,
,![]() 的最小二乘估计分别为
的最小二乘估计分别为 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据调查显示,某高校![]() 万男生的身高服从正态分布
万男生的身高服从正态分布![]() ,现从该校男生中随机抽取
,现从该校男生中随机抽取![]() 名进行身高测量,将测量结果分成
名进行身高测量,将测量结果分成![]() 组:
组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并绘制成如图所示的频率分布直方图.
,并绘制成如图所示的频率分布直方图.
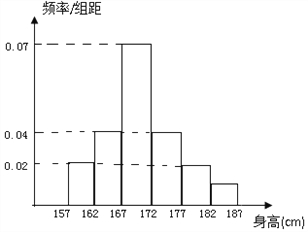
(Ⅰ)求这![]() 名男生中身高在
名男生中身高在![]() (含
(含![]() )以上的人数;
)以上的人数;
(Ⅱ)从这![]() 名男生中身高在
名男生中身高在![]() 以上(含
以上(含![]() )的人中任意抽取
)的人中任意抽取![]() 人,该
人,该![]() 人中身高排名(从高到低)在全校前
人中身高排名(从高到低)在全校前![]() 名的人数记为
名的人数记为![]() ,求
,求![]() 的数学期望.
的数学期望.
(附:参考数据:若![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
, ![]() ,
, ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() =(sinx,cosx),
=(sinx,cosx),![]() =(sin(x﹣
=(sin(x﹣![]() ),sinx),函数f(x)=2
),sinx),函数f(x)=2![]()
![]() ,g(x)=f(
,g(x)=f(![]() ).
).
(1)求f(x)在[![]() ,π]上的最值,并求出相应的x的值;
,π]上的最值,并求出相应的x的值;
(2)计算g(1)+g(2)+g(3)+…+g(2014)的值;
(3)已知t∈R,讨论g(x)在[t,t+2]上零点的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com