
【题目】有人玩掷均匀硬币走跳棋的游戏,棋盘上标有第0站(出发地),第1站,第2站,……,第100站. 一枚棋子开始在出发地,棋手每掷一次硬币,这枚棋子向前跳动一次,若掷出正向,棋子向前跳一站,若掷出反面,棋子向前跳两站,直到棋子跳到第99站(获胜)或跳到第100站(失败)时,该游戏结束. 设棋子跳到第![]() 站的概率为
站的概率为![]() .
.
(1)求![]() ,
,![]() ,
,![]() ,并根据棋子跳到第
,并根据棋子跳到第![]() 站的情况写出
站的情况写出![]() 与
与![]() 、
、![]() 的递推关系式(
的递推关系式(![]() );
);
(2)求证:数列![]()
![]() 为等比数列;
为等比数列;
(3)求玩该游戏获胜的概率.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
(1)棋子开始在第0站是必然事件,![]() ;棋子跳到第1站,
;棋子跳到第1站,![]() ;棋子跳到第2站,有两种情况,是互斥事件,分别求出,相加即可;依题意知,棋子跳到第
;棋子跳到第2站,有两种情况,是互斥事件,分别求出,相加即可;依题意知,棋子跳到第![]() (
(![]() )站有两种情况:棋子先跳到
)站有两种情况:棋子先跳到![]() 站和棋子先跳到
站和棋子先跳到![]() 站,它们是互斥事件,根据互斥事件的加法公式即得,
站,它们是互斥事件,根据互斥事件的加法公式即得,![]() (2)要证明数列
(2)要证明数列![]()
![]() 为等比数列,需证明
为等比数列,需证明![]() 是常数,
是常数,
将![]() 两边同减去
两边同减去![]() ,构成
,构成![]()
![]() 即可;
即可;
(3)由(2)知,![]() 得,将
得,将![]() 的前99项相加即可
的前99项相加即可
解:(1)棋子开始在第0站是必然事件,![]() ;
;
棋子跳到第1站,只有一种情况,第一次掷硬币正面向上,其概率为![]()
![]() ;
;
棋子跳到第2站,有两种情况,
①第一次掷硬币反面向上,其概率为![]() ;
;
②前两次掷硬币都是正面向上,其概率为![]()
![]() ;
;
依题意知,棋子跳到第![]() (
(![]() )站有两种情况:
)站有两种情况:
第一种,棋子先跳到![]() 站,又掷出反面,其概率为
站,又掷出反面,其概率为![]() ;
;
第二种,棋子先跳到![]() 站,又掷出正面,其概率为
站,又掷出正面,其概率为![]() .
.
∴![]()
故有:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)由(1)知,![]() ,
,
![]() ,又
,又![]() ,
,
数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
(3)由(2)知,![]() ,
,
∴![]()
![]()
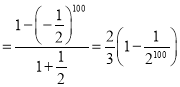 .
.
∴玩该游戏获胜的概率为![]()
故答案为:![]() .
.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】某城市的华为手机专卖店对该市市民使用华为手机的情况进行调查.在使用华为手机的用户中,随机抽取100名,按年龄(单位:岁)进行统计的频率分布直方图如图:

(1)根据频率分布直方图,分别求出样本的平均数(同一组数据用该区间的中点值作代表)和中位数的估计值(均精确到个位);
(2)在抽取的这100名市民中,按年龄进行分层抽样,抽取20人参加华为手机宣传活动,再从这20人中年龄在![]() 和
和![]() 的人群里,随机选取2人各赠送一部华为手机,求这2名市民年龄都在
的人群里,随机选取2人各赠送一部华为手机,求这2名市民年龄都在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出![]() 的极坐标方程和
的极坐标方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 、
、![]() 的极坐标分别为
的极坐标分别为![]() 和
和![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,射线
两点,射线![]() 与曲线
与曲线![]() 相交于点
相交于点![]() ,射线
,射线![]() 与曲线
与曲线![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解全校学生“体能达标”的情况,从全校1000名学生中随机选出40名学生,参加“体能达标”预测,并且规定“体能达标”预测成绩小于60分的为“不合格”,否则为“合格”若该校“不合格”的人数不超过总人数的![]() ,则全校“体能达标”为“合格”;否则该校“体能达标”为“不合格”,需要重新对全校学生加强训练现将这40名学生随机分为甲、乙两个组,其中甲组有24名学生,乙组有16名学生经过预测后,两组各自将预测成绩统计分析如下:甲组的平均成绩为70,标准差为4;乙组的平均成绩为80,标准差为6(题中所有数据的最后结果都精确到整数).
,则全校“体能达标”为“合格”;否则该校“体能达标”为“不合格”,需要重新对全校学生加强训练现将这40名学生随机分为甲、乙两个组,其中甲组有24名学生,乙组有16名学生经过预测后,两组各自将预测成绩统计分析如下:甲组的平均成绩为70,标准差为4;乙组的平均成绩为80,标准差为6(题中所有数据的最后结果都精确到整数).
(1)求这40名学生测试成绩的平均分![]() 和标准差
和标准差![]() ;
;
(2)假设该校学生的“体能达标”预测服从正态分布![]() 用样本平均数
用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() .利用估计值估计:该校学生“体能达标”预测是否“合格”?
.利用估计值估计:该校学生“体能达标”预测是否“合格”?
附:①![]() 个数
个数![]() 的平均数
的平均数![]() ,方差
,方差![]() ;
;
②若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障某治疗新冠肺炎药品的主要药理成分在国家药品监督管理局规定的值范围内,武汉某制药厂在该药品的生产过程中,检验员在一天中按照规定从该药品生产线上随机抽取20件产品进行检测,测量其主要药理成分含量(单位:mg).根据生产经验,可以认为这条药品生产线正常状态下生产的产品的主要药理成分含量服从正态分布N(μ,σ2).在一天内抽取的20件产品中,如果有一件出现了主要药理成分含量在(μ﹣3σ,μ+3σ)之外的药品,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对本次的生产过程进行检查.
(1)下面是检验员在2月24日抽取的20件药品的主要药理成分含量:
10.02 | 9.78 | 10.04 | 9.92 | 10.14 | 10.04 | 9.22 | 10.13 | 9.91 | 9.95 |
10.09 | 9.96 | 9.88 | 10.01 | 9.98 | 9.95 | 10.05 | 10.05 | 9.96 | 10.12 |
经计算得![]() xi=9.96,s
xi=9.96,s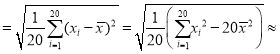 0.19;其中xi为抽取的第i件药品的主要药理成分含量,i=1,2,…,20.用样本平均数
0.19;其中xi为抽取的第i件药品的主要药理成分含量,i=1,2,…,20.用样本平均数![]() 作为μ的估计值
作为μ的估计值![]() ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值![]() ,利用估计值判断是否需对本次的生产过程进行检查?
,利用估计值判断是否需对本次的生产过程进行检查?
(2)假设生产状态正常,记X表示某天抽取的20件产品中其主要药理成分含量在(μ﹣3σ,μ+3σ)之外的药品件数,求/span>P(X=1)及X的数学期望.
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ﹣3σ<Z<μ+3σ)≈0.9974,0.997419≈0.95.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明,下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实,图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色其面积称为朱实,黄实,利朱用2×勾×股+(股-勾)2=4×朱实+黄实=弦实,化简得勾2+股2=弦2,设勾股中勾股比为![]() ,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
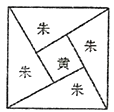
A.886B.500C.300D.134
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com