Question

14．方程cosx=-$\frac{x}{6}$的根的个数（　　）

• A． 2
• B． 3
• C． 4
• D． 5

Answer 1

分析 作函数y=cosx与函数y=-$\frac{x}{6}$的图象，结合图象可知函数的可能有4个交点，再对x∈[-2π，-$\frac{3π}{2}$）时，求导确定是否存在交点，从而解得．

解答 解：作函数y=cosx与函数y=-$\frac{x}{6}$的图象如下，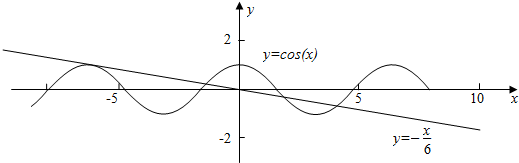
，
当x∈[-2π，-$\frac{3π}{2}$）时，令f（x）=cosx+$\frac{x}{6}$，
则f′（x）=-sinx+$\frac{1}{6}$，
令f′（x）=-sinx+$\frac{1}{6}$=0解得，
x=-2π+αrcsin$\frac{1}{6}$，
故f（x）在[-2π，-2π+αrcsin$\frac{1}{6}$）上是增函数，在（-2π+αrcsin$\frac{1}{6}$，-$\frac{3π}{2}$）上是减函数，
故f_max（x）=f（-2π+αrcsin$\frac{1}{6}$）
=cos（-2π+αrcsin$\frac{1}{6}$）+$\frac{-2π+αrcsin\frac{1}{6}}{6}$，
=$\frac{\sqrt{35}}{6}$+$\frac{-2π+αrcsin\frac{1}{6}}{6}$，
∵$\sqrt{35}$+αrcsin$\frac{1}{6}$-2π＜0，
∴f_max（x）＜0；
结合图象可知，方程cosx=-$\frac{x}{6}$的根的个数为3，
故选：B．

点评 本题考查了数形结合的思想应用及导数的综合应用，关键在于判断是否相切．