
【题目】如图,四棱锥![]() 的底面
的底面![]() 是平行四边形,侧面
是平行四边形,侧面![]() 是边长为2的正三角形,
是边长为2的正三角形, ![]() ,
, ![]() .
.
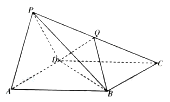
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)设![]() 是棱
是棱![]() 上的点,当
上的点,当![]() 平面
平面![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2acoskπlnx(k∈N*,a∈R且a>0).
(1)讨论函数f(x)的单调性;
(2)若k=2018,关于x的方程f(x)=2ax有唯一解,求a的值;
(3)当k=2019时,证明:对一切x∈(0,+∞),都有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝时期数学家、天文学家——祖暅,提出了著名的祖暅原理:“幂势既同,则积不容异也”.“幂”是截面积,“势”是几何体的高,意思是两等高几何体,若在每一等高处的两截面面积都相等,则两几何体体积相等.已知某不规则几何体与如图三视图所对应的几何体满足祖暅原理,则该不规则几何体的体积为( )
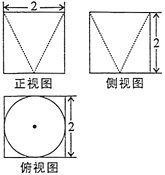
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以线段EF为直径的圆内切于圆O:x2+y2=16.
(1)若点F的坐标为(﹣2,0),求点E的轨迹C的方程;
(2)在(1)的条件下,轨迹C上存在点T,使得![]() ,其中M,N为直线y=kx+b(b≠0)与轨迹C的交点,求△MNT的面积.
,其中M,N为直线y=kx+b(b≠0)与轨迹C的交点,求△MNT的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】普通高中国家助学金,用于资助家庭困难的在校高中生.在本地,助学金分一等和二等两类,一等助学金每学期1250元,二等助学金每学期750元,并规定:属于农村建档立卡户的学生评一等助学金.某班有10名获得助学金的贫困学生,其中有3名属于农村建档立卡户,这10名学生中有4名获一等助学金,另6名获二等助学金.现从这10名学生中任选3名参加座谈会.
(Ⅰ)若事件A表示“选出的3名同学既有建档立卡户学生,又有非建档立卡户学生”,求A的概率;
(Ⅱ)设X为选出的3名同学一学期获助学金的总金额,求随机变量X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com