
【题目】已知函数f(x)=ex﹣ax+b.
(1)若f(x)在x=2有极小值1﹣e2 , 求实数a,b的值.
(2)若f(x)在定义域R内单调递增,求实数a的取值范围.
【答案】
(1)解:f′(x)=ex﹣a,
若f(x)在x=2有极小值1﹣e2,
则 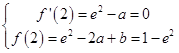 ,
,
解得: 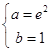
(2)解:∵f(x)=ex﹣ax+b,∴f'(x)=ex﹣a,
∵f(x)在R上单调递增,
∴f'(x)=ex﹣a≥0恒成立,
即a≤ex,x∈R恒成立.
∵x∈R时,ex∈(0,+∞),∴a≤0.
即a的取值范围为(﹣∞,0]
【解析】(1)求导函数,根据极值的意义得到关于a,b的方程组,求出a,b的值即可;(2)f(x)在R上单调递增,则f'(x)=ex﹣a≥0恒成立,分离参数,即可求得a的取值范围.
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的极值与导数,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值即可以解答此题.
是极小值即可以解答此题.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(2x﹣m)的定义域为集合A,函数g(x)= ![]() ﹣
﹣ ![]() 的定义域为集合B.
的定义域为集合B.
(Ⅰ)若BA,求实数m的取值范围;
(Ⅱ)若A∩B=,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,雾霾日趋严重,我们的工作、生活受到了严重的影响,如何改善空气质量已成为当今的热点问题.某空气净化器制造厂,决定投入生产某型号的空气净化器,根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产该型号空气净化器x(百台),其总成本为P(x)(万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本).销售收入Q(x)(万元)满足Q(x)= ![]() ,假定该产品产销平衡(即生产的产品都能卖掉),根据以述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据以述统计规律,请完成下列问题:
(1)求利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)工厂生产多少百台产品时,可使利润最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校一模考试数学测试成绩的茎叶图和频率分布直方图都受到不同程序的破坏,可见部分如下
试根据图表中的信息解答下列问题:
(1)求全班的学生人数及分数在 ![]() 之间的频数;
之间的频数;
(2)为快速了解学生的答题情况,老师按分层抽样的方法从位于 ![]() ,
, ![]() ,和
,和 ![]() 分数段的试卷中抽取8份进行分析,再从中任选2人进行交流,求交流的2名学生中,恰有一名成绩位于
分数段的试卷中抽取8份进行分析,再从中任选2人进行交流,求交流的2名学生中,恰有一名成绩位于 ![]() 分数段的概率.
分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足|x﹣1|>a其中a>0;命题q:实数x满足 ![]() <1
<1
(1)若命题p中a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() +
+ ![]() =1与x轴交于A、B两点,过椭圆上一点P(x0 , y0)(P不与A、B重合)的切线l的方程为
=1与x轴交于A、B两点,过椭圆上一点P(x0 , y0)(P不与A、B重合)的切线l的方程为 ![]() +
+ ![]() =1,过点A、B且垂直于x轴的垂线分别与l交于C、D两点,设CB、AD交于点Q,则点Q的轨迹方程为 .
=1,过点A、B且垂直于x轴的垂线分别与l交于C、D两点,设CB、AD交于点Q,则点Q的轨迹方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(1,2,-1),B(2,0,2).
(1)在x轴上求一点P,使|PA|=|PB|;
(2)若xOz平面内的点M到点A的距离与到点B的距离相等,求点M的坐标满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射击队有8名队员,其中男队员5名,女队员3名,从中随机选3名队员参加射击表演活动.
(1)求选出的3名队员中有一名女队员的概率;
(2)求选出的3名队员中女队员人数比男队员人数多的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com