
【题目】如图:在四棱锥V﹣ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为 ![]() 的等腰三角形.
的等腰三角形. 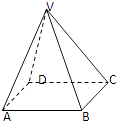
(1)求二面角V﹣AB﹣C的平面角的大小;
(2)求四棱锥V﹣ABCD的体积.
【答案】
(1)解:取AB的中点M,CD的中点N,连MN、VM、VN,
∵底面ABCD是边长为2的正方形,∴MN⊥AB,MN=2
又∵VA=VB= ![]() ,M为AB的中点,∴VM⊥AB
,M为AB的中点,∴VM⊥AB
∴∠VMN是二面角V﹣AB﹣C的平面角
在Rt△VAM中,AM=1,VA= ![]() ,
,
∴VM= ![]() =2,同理可得VN=2
=2,同理可得VN=2
∴△VMN是正三角形,可得∠VMN=60°
即二面角V﹣AB﹣C的大小为60°
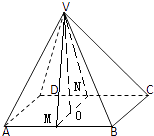
(2)解:由(1)知AB⊥平面VMN
∵AB平面ABCD,∴平面ABCD⊥平面VMN
过V作VO⊥MN于点O,
∵平面ABCD⊥平面VMN,平面ABCD∩平面VMN=MN,VO平面VMN
∴VO⊥平面ABCD,得VO是四棱锥V﹣ABCD的高
∵VM=MN=NV=2,∴VO= ![]()
因此,四棱锥V﹣ABCD的体积为
V= ![]() SABCD×VO=
SABCD×VO= ![]() =
= ![]()
【解析】(1)取AB的中点M,CD的中点N,连MN、VM、VN.利用正方形的性质和等腰三角形的“三线合一”,证出MN⊥AB且VM⊥AB,得到∠VMN是二面角V﹣AB﹣C的平面角.再根据题中数据算出△VMN是正三角形,得∠VMN=60°,即得二面角V﹣AB﹣C的大小;(2)过V作VO⊥MN于点O,利用面面垂直的性质与判定证出VO⊥平面ABCD,得VO是四棱锥V﹣ABCD的高.正三角形△VMN中算出VO的长,结合锥体的体积公式和题中的数据,即可得到四棱锥V﹣ABCD的体积.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按照5天一组分组统计,绘制了频率分布直方图(如图所示).已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列各题.

(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件2件作品获奖,问这两组哪一组获奖率较高?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1在平面直角坐标系中的参数方程为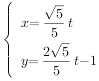 (t为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,有曲线C2:ρ=2cosθ-4sinθ
(t为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,有曲线C2:ρ=2cosθ-4sinθ
(1)将C1的方程化为普通方程,并求出C2的平面直角坐标方程
(2)求曲线C1和C2两交点之间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中,a1=1,Sn表示前n项和,且Sn , Sn+1 , 2S1成等差数列.
(1)计算S1 , S2 , S3的值;
(2)根据以上结果猜测Sn的表达式,并用数学归纳法证明你的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(sinx+cosx)2+2cos2x
(1)求函数f(x)的最小正周期和单调减区间;
(2)求使f(x)≥3成立的x的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(3ωx+ ![]() ),其中ω>0
),其中ω>0
(1)若f(x+θ)是周期为2π的偶函数,求ω及θ的值;
(2)若f(x)在(0, ![]() ]上是增函数,求ω的最大值;
]上是增函数,求ω的最大值;
(3)当ω= ![]() 时,将函数f(x)的图象向右平移
时,将函数f(x)的图象向右平移 ![]() 个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 
(1)当x≤0时,解不等式f(x)≥﹣1;
(2)写出该函数的单调区间;
(3)若函数g(x)=f(x)﹣m恰有3个不同零点,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com