[题目]祖暅原理:“幂势既同.则积不容异．它是中国古代一个涉及几何体体积的问题.意思是两个同高的几何体.如在等高处的截面积恒相等.则体积相等．设为两个同高的几何体.的体积不相等.在等高处的截面积不恒相等.根据祖暅原理可知.是的( )A. 充分不必要条件 B. 必要不充分条件C. 充要条件 D. 既不充分也不必要条件题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】祖暅原理：“幂势既同，则积不容异”．它是中国古代一个涉及几何体体积的问题，意思是两个同高的几何体，如在等高处的截面积恒相等，则体积相等．设为两个同高的几何体，的体积不相等，在等高处的截面积不恒相等，根据祖暅原理可知，是的（）

A. 充分不必要条件 B. 必要不充分条件

C. 充要条件 D. 既不充分也不必要条件

【答案】A

【解析】设命题：“若，则”.可知命题是祖暅原理的逆否命题，由命题的性质可知必然成立.故是的充分条件；

设命题：“若，则”，对此可以举出反例，若比在某些等高处的截面积小一些，在另一些等高处的截面积多一些，且多的总量与少的总量相抵，则它们的体积还是一样的.所以命题：“若，则”是假命题，即不是的必要条件.

综上所述，是的充分不必要条件.

故本题正确答案为

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知两圆C1：x2＋y2－2x－6y－1＝0和C2：x2＋y2－10x－12y＋45＝0.

(1)求证：圆C1和圆C2相交；

(2)求圆C1和圆C2的公共弦所在直线的方程和公共弦长．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f(x)＝x2－1，g(x)＝

(1)求f[g(2)]和g[f(2)]的值；

(2)求f[g(x)]和g[f(x)]的表达式．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】（本小题满分12分）

甲乙两个班级进行一门课程的考试，按照学生考试成绩优秀和不优秀统计成绩后，得到如下的列联表：

班级与成绩列联表

	优秀	不优秀
甲班	10	35
乙班	7	38

根据列联表的独立性检验，能否在犯错误的概率不超过0.01的前提下认为成绩与班级有关系？

附：

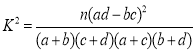
	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某公司在迎新年晚会上举行抽奖活动，有甲、乙两个抽奖方案供员工选择；

方案甲：员工最多有两次抽奖机会，每次抽奖的中奖率为.第一次抽奖，若未中奖，则抽奖结束.若中奖，则通过抛一枚质地均匀的硬币，决定是否继续进行第二次抽奖，规定：若抛出硬币，反面朝上，员工则获得500元奖金，不进行第二次抽奖；若正面朝上，员工则须进行第二次抽奖，且在第二次抽奖中，若中奖，获得奖金1000元；若未中奖，则所获奖金为0元.