【题目】已知函数
（
）.
（Ⅰ）当
时，判断函数
的零点个数；
（Ⅱ）若
，求
的最大值.
【答案】（Ⅰ）1；（Ⅱ） 
．
【解析】试题分析：
(1)由导函数结合函数的极值可得函数
在
内有且只有一个零点；
(2) 构造函数
，
若
，不符合题意，讨论
可得
，
二次构造函数
，结合函数的性质可得
的最大值为
.
试题解析：
（Ⅰ）当
时， 
，定义域为
，
当
时， 
，所以函数
在
内无零点；
当
时， 
，因为
， 
，所以
，说明函数
在
上单调递减，又
，当
时， 
，所以函数
在
内有且只有一个零点；
综上，函数
的零点个数是1；
（Ⅱ）若
，即
，设
，
若
，则当
时，显然
，故不符合题意，所以
.
（
），
当
时， 
，所以
在
上单调递增；
当
时， 
，所以
在
上单调递减；
从而
，
由题意可知
，所以
，
此时
，令
， 
，
可知
在
上单调增，在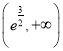
上单调减，
所以
，故
的最大值为
.
举一反三期末百分冲刺卷系列答案科目：高中数学 来源： 题型：
【题目】某手机卖场对市民进行国产手机认可度的调查，随机抽取
名市民，按年龄（单位：岁）进行统计和频数分布表和频率分布直线图如下：
分组（岁） | 频数 |
|
|
|
|
|
|
|
|
|
|
合计 |
|
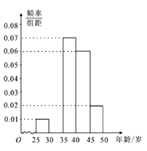
（1）求频率分布表中
、
的值，并补全频率分布直方图；
（2）在抽取的这
名市民中，按年龄进行分层抽样，抽取
人参加国产手机用户体验问卷调查，现从这
人中随机选取
人各赠送精美礼品一份，设这
名市民中年龄在
内的人数
，求
的分布列及数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
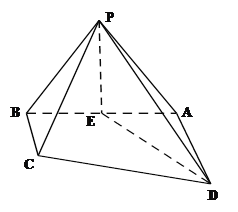
【题目】如图，四棱锥P—ABCD中，底面ABCD是直角梯形，∠DAB=90°，AD//BC，且BC⊥PB，△PAB是等边三角形，DA=AB=2，BC=
AD，E是线段AB的中点.
（I）求证：PE⊥CD；
（II）求PC与平面PDE所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆
经过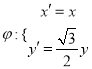
变换后得曲线
.
（1）求
的方程；
（2）若
为曲线
上两点， 
为坐标原点，直线
的斜率分别为
且
，求直线
被圆
截得弦长的最大值及此时直线
的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P﹣ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．
（1）求PB和平面PAD所成的角的大小；
（2）证明AE⊥平面PCD．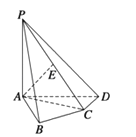
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个多面体的直观图，正（主）视图，侧（左）视图如下所示，其中正（主）视图、侧（左）视图为边长为a的正方形．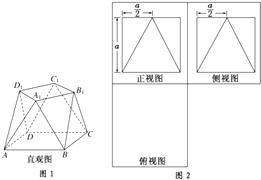 
（1）请在指定的框内画出多面体的俯视图；
（2）若多面体底面对角线AC，BD交于点O，E为线段AA1的中点，求证：OE∥平面A1C1C；
（3）求该多面体的表面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
（a＞0）．
（1）证明函数f（x）在（0，2]上是减函数，（2，+∞）上是增函数；
（2）若方程f（x）=0有且只有一个实数根，判断函数g（x）=f（x）﹣4的奇偶性；
（3）在（2）的条件下探求方程f（x）=m（m≥8）的根的个数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
