某家庭为小孩买教育保险,小孩在出生的第一年父母就交纳保险金,数目为a1,以后每年交纳的数目均比上一年增加d(d>0),因此,历年所交纳的保险金数目为a1,a2,…是一个公差为d的等差数列,与此同时保险公司给予优惠的利息政策,不仅采用固定利率,而且计算复利,这就是说,如果固定利率为r(r>0),那么,在第n年末,第一年所交纳的保险金就变为a1(1+r)n-1,第二年所交纳的保险金就变为a2(1+r)n-2,…,以Tn表示到第n年末所累计的保险金总额.
(1)写出Tn与Tn+1的递推关系(n≥1);
(2)若a1=1,d=0.1,求{Tn}的通项公式.(用r表示)
【答案】
分析:(1)通过已知条件求出等差数列的通项公式,然后根据条件写出T
n与T
n+1的递推关系(n≥1);
(2)通过(1)的递推关系式,利用待定系数法,构造新数列,求出数列的通项公式,即可得到{T
n}的通项公式.
解答:解:(1)因为数目为a
1,以后每年交纳的数目均比上一年增加d(d>0),
因此,历年所交纳的保险金数目为a
1,a
2,…是一个公差为d的等差数列,所以a
n=a
1+nd,
与此同时保险公司给予优惠的利息政策,不仅采用固定利率,而且计算复利,
这就是说,如果固定利率为r(r>0),
那么,在第n年末,第一年所交纳的保险金就变为a
1(1+r)
n-1,
第二年所交纳的保险金就变为a
2(1+r)
n-2,…,所以T
n=T
n-1(1+r)+a
n(n≥2).
∴T
n+1=T
n(1+r)+a
1+nd (6分)
(2)T
n+1=T
n(1+r)+
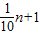
,T
1=a
1=1
用待定系数法:T
n+1+A(n+1)+B=(1+r)(T
n+An+B)
解得:A=
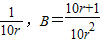
,所以{T
n+
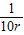
n+
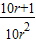
}是以1为首项以1+r为公比的等比数列,
∴T
n+

n+
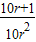
=
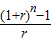
解得:T
n=
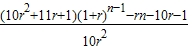
(7分)
点评:本题考查数列模型的构建,考查等比数列求和的基本方法的运用,解题的关键是正确构建数列模型.

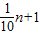 ,T1=a1=1
,T1=a1=1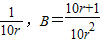 ,所以{Tn+
,所以{Tn+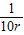 n+
n+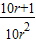 }是以1为首项以1+r为公比的等比数列,
}是以1为首项以1+r为公比的等比数列, n+
n+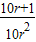 =
=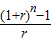
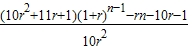 (7分)
(7分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案