
【题目】选修4-5:不等式选讲
已知函数![]() .
.
(I)求证:![]() 恒成立;
恒成立;
(II)若存在实数![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班极工作的态度是否有关系?请说明理由.
附:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
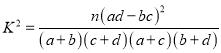
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一名学生每天骑车上学,从他家里到学校的途中有6个交通岗,假设在每个交通岗遇到红灯的事件是相互独立的,并且概率都是![]() .
.
(1)假设![]() 为这名学生在途中遇到红灯的次数,求
为这名学生在途中遇到红灯的次数,求![]() 的分布列;
的分布列;
(2)设![]() 为这名学生在首次停车前经过的路口数,求
为这名学生在首次停车前经过的路口数,求![]() 的分布列;
的分布列;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如下:

试根据图表中的信息解答下列问题:
(1)求全班的学生人数及分数在[70,80)之间的频数;
(2)为快速了解学生的答题情况,老师按分层抽样的方法从位于[70,80),[80,90)和[90,100]分数段的试卷中抽取8份进行分析,再从中任选3人进行交流,求交流的学生中,成绩位于[70,80)分数段的人数X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,连接椭圆的四个顶点得到的四边形的面积为
,连接椭圆的四个顶点得到的四边形的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左焦点为
的左焦点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 过点
过点![]() 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线![]() 垂直
垂直![]() 于点
于点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,求点
,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)设![]() 为坐标原点,取
为坐标原点,取![]() 上不同于
上不同于![]() 的点
的点![]() ,以
,以![]() 为直径作圆与
为直径作圆与![]() 相交另外一点
相交另外一点![]() ,求该圆面积的最小值时点
,求该圆面积的最小值时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府调查了工薪阶层![]() 人的月工资收人,并根据调查结果画出如图所示的频率分布直方图,其中工资收人分组区间是
人的月工资收人,并根据调查结果画出如图所示的频率分布直方图,其中工资收人分组区间是![]() .(单位:百元)
.(单位:百元)

(1)为了了解工薪阶层对工资收人的满意程度,要用分层抽样的方法从调查的![]() 人中抽取
人中抽取![]() 人做电话询问,求月工资收人在
人做电话询问,求月工资收人在![]() 内应抽取的人数;
内应抽取的人数;
(2)根据频率分布直方图估计这![]() 人的平均月工资为多少元.
人的平均月工资为多少元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com