【题目】某种产品按质量标准分为
,
,
,
,
五个等级.现从一批该产品随机抽取20个，对其等级进行统计分析，得到频率分布表如下：
等级 |
|
|
|
|
|
频率 |
|
|
|
|
|
（1）在抽取的20个产品中，等级为5的恰有2个，求
,
；
（2）在（1）的条件下，从等级为3和5的所有产品中，任意抽取2个，求抽取的2个产品等级恰好相同的概率.
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案科目：高中数学 来源： 题型：
【题目】家政服务公司根据用户满意程度将本公司家政服务员分为两类，其中A类服务员12名，B类服务员x名．
(Ⅰ)若采用分层抽样的方法随机抽取20名家政服务员参加技术培训，抽取到B类服务员的人数是16, 求x的值；
(Ⅱ)某客户来公司聘请2名家政服务员，但是由于公司人员安排已经接近饱和，只有3名A类家政服务员和2名B类家政服务员可供选择，求该客户最终聘请的家政服务员中既有A类又有B类的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
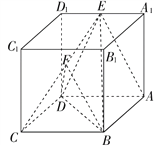
【题目】如图，正方体ABCD－A1B1C1D1中，点E是A1D1的中点，点F是CE的中点．
(Ⅰ)求证：平面ACE⊥平面BDD1B1；
(Ⅱ)求证：AE∥平面BDF.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是菱形，PD⊥平面ABCD，PD=AD=3，PM=2MD，AN=2NB，∠DAB=60°．
（1）求证：直线AM∥平面PNC；
（2）求二面角D﹣PC﹣N的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
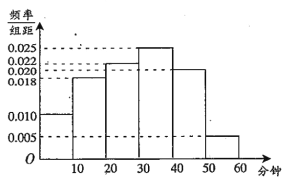
【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系，对该校200名学生的课外体育锻炼平均每天运动的时间（单位：分钟）进行调查，将收集的数据分成
六组，并作出频率分布直方图（如图），将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
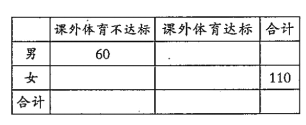
(1)请根据直方图中的数据填写下面的
列联表，并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关？
（2）在[0，10），[40，50）这两组中采取分层抽样，抽取6人，再从这6名学生中随机抽取2人参加体育知识问卷调查，求这2人中一人来自“课外体育达标”和一人来自“课外体育不达标”的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
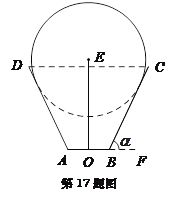
【题目】一儿童游乐场拟建造一个“蛋筒”型游乐设施，其轴截面如图中实线所示. 
是等腰梯形， 
米， 
（
在
的延长线上， 
为锐角）. 圆
与
都相切，且其半径长为
米. 
是垂直于
的一个立柱，则当
的值设计为多少时，立柱
最矮？
查看答案和解析>>
科目：高中数学 来源： 题型：
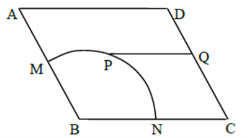
【题目】如图，某广场中间有一块边长为2百米的菱形状绿化区
，其中
是半径为1百米的扇形，
． 管理部门欲在该地从
到
修建小路：在弧
上选一点
（异于
两点），过点
修建与
平行的小路
．问：点
选择在何处时，才能使得修建的小路
与
及
的总长最小？并说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(导学号：05856323)已知在△ABC中，A，B，C所对的边分别为a，b，c，R为△ABC外接圆的半径，若a＝1， 
sin2B＋
sin2C－sin2A＝sin Asin Bsin C，则R的值为( )
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
