
【题目】如图所示,已知AB为圆O的直径,C,D是圆O上的两个点,CE⊥AB于E,BD交AC于G,交CE于F,CF=FG. 
(1)求证:AC是∠DAB的平分线;
(2)求证:OF∥AG.
【答案】
(1)解:∵CF=FG
∴∠CGF=∠FCG
∴AB圆O的直径
∴∠ACB=∠ADB=90°
∵CE⊥AB
∴∠CEA=90°
∵∠CBA=90°﹣∠CAB,∠ACE=90°﹣∠CAB
∴∠CBA=∠ACE
∵∠CGF=∠DGA,
∴∠DGA=∠ABC
∴∴∠CAB=∠DAC
∴C为劣弧BD的中点,
∴AC是∠DAB的平分线;
(2)解:∵∠GBC=90°﹣∠CGB,∠FCB=90°﹣∠GCF
∴∠GBC=∠FCB
∴CF=FB
同理可证:CF=GF
∴BF=FG,
∵OA=OB,
∴OF∥AG.
【解析】(1)要证明C是劣弧BD的中点,即证明弧BC与弧CD相等,即证明∠CAB=∠DAC,根据已知中CF=FG,AB是圆O的直径,CE⊥AB于E,我们易根据同角的余角相等,得到结论.(2)由已知及(I)的结论,我们易证明△BFC及△GFC均为等腰三角形,即CF=BF,CF=GF,进而得到结论.


科目:高中数学 来源: 题型:
【题目】遂宁市观音湖港口船舶停靠的方案是先到先停.
(1)若甲乙两艘船同时到达港口,双方约定各派一名代表从1,2,3,4,5中各随机选一个数(甲、乙选取的数互不影响),若两数之和为偶数,则甲先停靠;若两数之和为奇数,则乙先停靠,这种规则是否公平?请说明理由.
(2)根据以往经验,甲船将于早上7:00~8:00到达,乙船将于早上7:30~8:30到达,请求出甲船先停靠的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,空间四边形ABCD的对棱AD、BC成600的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.
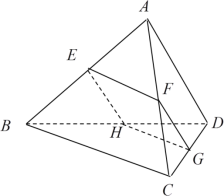
(1)求证:四边形EFGH为平行四边形;
(2)E在AB的何处时截面EFGH的面积最大?最大面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品在近30天内每件的销售价格P元和时间t(t∈N)的关系如图所示.
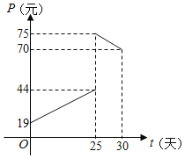
(1)请确定销售价格P(元)和时间t(天)的函数解析式;
(2)该商品的日销售量Q(件)与时间t(天)的关系是:Q=﹣t+40(0≤t≤30,t∈N),求该商品的日销售金额y(元)与时间t(天)的函数解析式;
(3)求该商品的日销售金额y(元)的最大值,并指出日销售金额最大的一天是30天中的哪一天?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点O,焦点在x轴上的椭圆的一个顶点坐标为(2,0),离心率为 ![]()

(1)求椭圆的方程;
(2)若A(0,1),设M,N是椭圆上异于点A的任意两点,且AM⊥AN,线段MN的中垂线l与x轴的交点为(m,0),求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有A、B两家羽毛球球俱乐部,两家设备和服务都很好,但收费方式不同,A俱乐部每块场地每小时收费6元;B俱乐部按月计费,一个月中20小时以内![]() 含20小时
含20小时![]() 每块场地收费90元,超过20小时的部分,每块场地每小时2元,某企业准备下个月从这两家俱乐部中的一家租用一块场地开展活动,其活动时间不少于12小时,也不超过30小时.
每块场地收费90元,超过20小时的部分,每块场地每小时2元,某企业准备下个月从这两家俱乐部中的一家租用一块场地开展活动,其活动时间不少于12小时,也不超过30小时.
![]() 设在A俱乐部租一块场地开展活动x小时的收费为
设在A俱乐部租一块场地开展活动x小时的收费为![]() 元
元![]() ,在B俱乐部租一块场地开展活动x小时的收费为
,在B俱乐部租一块场地开展活动x小时的收费为![]() 元
元![]() ,试求
,试求![]() 与
与![]() 的解析式;
的解析式;
![]() 问该企业选择哪家俱乐部比较合算,为什么?
问该企业选择哪家俱乐部比较合算,为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,并且满足
,并且满足![]() ,
, ![]() .
.
(1)求数列![]() 通项公式;
通项公式;
(2)设![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证: ![]() .
.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】试题分析:(1)根据题意得到![]() ,
, ![]() ,两式做差得到
,两式做差得到![]() ;(2)根据第一问得到
;(2)根据第一问得到![]() ,由错位相减法得到前n项和,进而可证和小于1.
,由错位相减法得到前n项和,进而可证和小于1.
解析:
(1)∵![]()
当![]() 时,
时, ![]()
当![]() 时,
时, ![]() ,即
,即![]()
∴数列![]() 时以
时以![]() 为首项,
为首项, ![]() 为公差的等差数列.
为公差的等差数列.
∴![]() .
.
(2)∵![]()
∴![]() ①
①
![]() ②
②
由①![]() ②得
②得
![]()
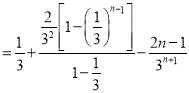
![]()
∴![]()
点睛:这个题目考查的是数列通项公式的求法及数列求和的常用方法;数列通项的求法中有常见的已知![]() 和
和![]() 的关系,求
的关系,求![]() 表达式,一般是写出
表达式,一般是写出![]() 做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等.
做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等.
【题型】解答题
【结束】
22
【题目】已知![]() ,
, ![]() 分别是椭圆
分别是椭圆![]() :
: ![]() (
(![]() )的左、右焦点,
)的左、右焦点, ![]() 是椭圆
是椭圆![]() 上的一点,且
上的一点,且![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() ,
, ![]() ,椭圆
,椭圆![]() 上存在点
上存在点![]() ,使得以
,使得以![]() ,
, ![]() 为邻边的四边形
为邻边的四边形![]() 为平行四边形(
为平行四边形(![]() 为坐标原点).
为坐标原点).
(ⅰ)求实数![]() 与
与![]() 的关系;
的关系;
(ⅱ)证明:四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com