
【题目】对于函数![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的“不动点”,若
的“不动点”,若![]() ,则称
,则称![]() 为
为![]() 的“稳定点”,函数
的“稳定点”,函数![]() 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为![]() 和
和![]() ,即
,即![]() ,
,![]() ,那么,
,那么,
(1)求函数![]() 的“稳定点”;
的“稳定点”;
(2)求证:![]() ;
;
(3)若![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)“稳定点”为![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
本题拿出一个概念来作为新型定义题,只需要去对定义的理解就好,要求函数![]() 的“稳定点”只需求方程
的“稳定点”只需求方程![]() 中
中![]() 的值,即为“稳定点”
的值,即为“稳定点”
若![]() ,有
,有![]() 这是不动点的定义,此时得出
这是不动点的定义,此时得出![]() ,
,![]() ,如果
,如果![]() ,则直接满足.
,则直接满足.
先求出![]() 即
即![]() 存在“不动点”的条件,同理取得到存在“稳定点”的条件,而两集合相等,即条件所求出的结果一直,对结果进行分类讨论.
存在“不动点”的条件,同理取得到存在“稳定点”的条件,而两集合相等,即条件所求出的结果一直,对结果进行分类讨论.
(1)由![]() 有
有![]() ,得:
,得:![]() ,所以函数
,所以函数![]() 的“稳定点”为
的“稳定点”为![]() ;
;
(2)证明:若![]() ,则
,则![]() ,显然成立;
,显然成立;
若![]() ,设
,设![]() ,有
,有![]() ,则有
,则有![]() ,
,
所以![]() ,故
,故![]()
(3)因为![]() ,所以方程
,所以方程![]() 有实根,即
有实根,即![]() 有实根,
有实根,
所以![]() 或
或![]() ,解得
,解得![]() 又由
又由![]() 得:
得:![]() 即
即![]() 由(1)知
由(1)知![]() ,故方程
,故方程![]() 左边含有因式
左边含有因式![]()
所以![]() ,又
,又![]() ,
,
所以方程![]() 要么无实根,要么根是方程
要么无实根,要么根是方程![]() 的解,
的解,
当方程![]() 无实根时,
无实根时,![]() 或
或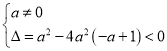 ,即
,即![]() ,
,
当方程![]() 有实根时,则方程
有实根时,则方程![]() 的根是方程
的根是方程![]() 的解,
的解,
则有![]() ,代入方程
,代入方程![]() 得
得![]() ,故
,故![]() ,
,
将![]() 代入方程
代入方程![]() ,得
,得![]() ,所以
,所以![]() .
.
综上:![]() 的取值范围是
的取值范围是![]() .
.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案科目:高中数学 来源: 题型:
【题目】某二手交易市场对某型号的二手汽车的使用年数![]() (
(![]() )与销售价格
)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
销售价格 | 16 | 13 | 9.5 | 7 | 4.5 |
(I)试求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() .
.
(参考公式: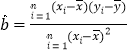 ,
,![]() )
)
(II)已知每辆该型号汽车的收购价格为![]() 万元,根据(I)中所求的回归方程,预测
万元,根据(I)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?(利润=销售价格-收购价格)
最大?(利润=销售价格-收购价格)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
API | [0,100] | (100,200] | (200,300] | >300 |
空气质量 | 优良 | 轻污染 | 中度污染 | 重度污染 |
天数 | 17 | 45 | 18 | 20 |
记某企业每天由空气污染造成的经济损失S(单位:元),空气质量指数API为![]() .当
.当![]() 时,企业没有造成经济损失;当
时,企业没有造成经济损失;当![]() 对企业造成经济损失成直线模型(当
对企业造成经济损失成直线模型(当![]() 时造成的经济损失为
时造成的经济损失为![]() ,当
,当![]() 时,造成的经济损失
时,造成的经济损失![]() );当
);当![]() 时造成的经济损失为2000元;
时造成的经济损失为2000元;
(1)试写出![]() 的表达式;
的表达式;
(2)若本次抽取的样本数据有30天是在供暖季,其中有12天为重度污染,完成下面2×2列联表,并判断能否有99%的把握认为该市本年空气重度污染与供暖有关?
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
![]()
P(k2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱柱ABCD﹣A1B1C1D1(底面是正方形,侧棱垂直于底面)的8个顶点都在球O的表面上,AB=1,AA1′=2,则球O的半径R=;若E,F是棱AA1和DD1的中点,则直线EF被球O截得的线段长为 . 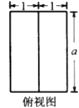
查看答案和解析>>
科目:高中数学 来源: 题型:
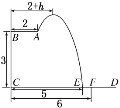
【题目】某跳水运动员在一次跳水训练时的跳水曲线为如图所示抛物线的一段.已知跳水板![]() 长为
长为![]() ,跳水板距水面
,跳水板距水面![]() 的高
的高![]() 为
为![]() .为安全和空中姿态优美,训练时跳水曲线应在离起跳点
.为安全和空中姿态优美,训练时跳水曲线应在离起跳点![]() 处水平距
处水平距![]()
![]() 时达到距水面最大高度
时达到距水面最大高度![]() ,规定:以
,规定:以![]() 为横轴,
为横轴,![]() 为纵轴建立直角坐标系.
为纵轴建立直角坐标系.
(1)当![]() 时,求跳水曲线所在的抛物线方程;
时,求跳水曲线所在的抛物线方程;
(2)若跳水运动员在区域![]() 内入水时才能达到比较好的训练效果,求此时
内入水时才能达到比较好的训练效果,求此时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E,F分别是棱A1B1 , B1C1的中点,O是AC与BD的交点,面OEF与面BCC1B1相交于m,面OD1E与面BCC1B1相交于n,则直线m,n的夹角为( )
A.0
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com