
【题目】已知a,b,c分别是△ABC的角A,B,C所对的边,且c=2,C= ![]() .
.
(1)若△ABC的面积等于 ![]() ,求a,b;
,求a,b;
(2)若sinC+sin(B﹣A)=2sin2A,求A的值.
【答案】
(1)解:∵c=2,C= ![]() ,由余弦定理可得:c2=a2+b2﹣2abcosC,
,由余弦定理可得:c2=a2+b2﹣2abcosC,
∴4=a2+b2﹣ab,
∵ ![]() =
= ![]() ,化为ab=4.
,化为ab=4.
联立 ![]() ,解得a=2,b=2
,解得a=2,b=2
(2)解:∵sinC=sin(B+A),sinC+sin(B﹣A)=2sin2A,
∴sin(A+B)+sin(B﹣A)=2sin2A,
2sinBcosA=4sinAcosA,
当cosA=0时,解得A= ![]() ;
;
当cosA≠0时,sinB=2sinA,
由正弦定理可得:b=2a,
联立 ![]() ,解得
,解得 ![]() ,b=
,b= ![]() ,
,
∴b2=a2+c2,
∴ ![]() ,
,
又 ![]() ,∴
,∴ ![]() .
.
综上可得:A= ![]() 或
或 ![]()
【解析】(1)c=2,C= ![]() ,由余弦定理可得:c2=a2+b2﹣2abcosC,即4=a2+b2﹣ab,利用三角形面积计算公式
,由余弦定理可得:c2=a2+b2﹣2abcosC,即4=a2+b2﹣ab,利用三角形面积计算公式 ![]() =
= ![]() ,即ab=4.联立解出即可.(2)由sinC=sin(B+A),sinC+sin(B﹣A)=2sin2A,可得2sinBcosA=4sinAcosA.当cosA=0时,解得A=
,即ab=4.联立解出即可.(2)由sinC=sin(B+A),sinC+sin(B﹣A)=2sin2A,可得2sinBcosA=4sinAcosA.当cosA=0时,解得A= ![]() ;当cosA≠0时,sinB=2sinA,由正弦定理可得:b=2a,联立解得即可.
;当cosA≠0时,sinB=2sinA,由正弦定理可得:b=2a,联立解得即可.


科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足,a2=3,a5=81.
(1)求数列{an}的通项公式;
(2)设bn=log3an , 求{bn}的前n项和为Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+bx,则“b<0”是“f(f(x))的最小值与f(x)的最小值相等”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn满足Sn= ![]() n2+
n2+ ![]() n(n∈N*),数列{bn}是首项为4的正项等比数列,且2b2 , b3﹣3,b2+2成等差数列. (Ⅰ)求数列{an},{bn}的通项公式;
n(n∈N*),数列{bn}是首项为4的正项等比数列,且2b2 , b3﹣3,b2+2成等差数列. (Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)令cn=anbn(n∈N*),求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家实施二孩放开政策后,为了了解人们对此政策持支持态度是否与年龄有关,计生部门将已婚且育有一孩的居民分成中老年组(45岁以上,含45岁)和中青年组(45岁以下,不含45岁)两个组别,每组各随机调查了50人,对各组中持支持态度和不支持态度的人所占的频率绘制成等高条形图,如图所示: 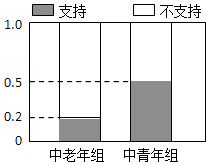
支持 | 不支持 | 合计 | |
中老年组 | 50 | ||
中青年组 | 50 | ||
合 计 | 100 |
(1)根据以上信息完成2×2列联表;
(2)是否有99%以上的把握认为人们对此政策持支持态度与年龄有关?
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
附: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0),过其焦点F的直线l交抛物线C于点A、B,|AF|=3|BF|,则|AB|=( )
A.p
B.![]()
C.2p
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com