
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.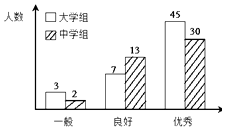
(Ⅰ)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的2×2列联表,并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
优秀 | 合格 | 合计 | |
大学组 | |||
中学组 | |||
合计 |
注:K2 ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(k2≥k0) | 0.10 | 0.05 | 0.005 |
k0 | 2.706 | 3.841 | 7.879 |
(Ⅱ)若江西参赛选手共80人,用频率估计概率,试估计其中优秀等级的选手人数;
(Ⅲ)如果在优秀等级的选手中取4名,在良好等级的选手中取2名,再从这6人中任选3人组成一个比赛团队,求所选团队中的有2名选手的等级为优秀的概率.
【答案】解:(Ⅰ)由条形图知2×2列联表如下:
优秀 | 合格 | 合计 | |
大学组 | 45 | 10 | 55 |
中学组 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
∴K2= ![]() =
= ![]() ,
,
∴没有95%的把握认为选手成绩“优秀”与文化程度有关.
(Ⅱ)由条形图知,所抽取的100人中,优秀等级有75人,故优秀率为 ![]() =
= ![]() ,
,
∴参赛选手中优秀等级的选手人数估计为:80× ![]() =60人.
=60人.
(Ⅲ)在优秀等级的选手中取4名,在良好等级的选手中取2名,
再从这6人中任选3人组成一个比赛团队,
基本事件总数n= ![]() =20,
=20,
所选团队中的有2名选手的等级为优秀包含的基本事件个数m= ![]() =6,
=6,
∴所选团队中的有2名选手的等级为优秀的概率p= ![]() .
.
【解析】(1)由条形图得到2×2列联表,计算出K2,可得出没有95%的把握认为选手成绩“优秀”与文化程度有关.(2)由条形图知所抽取的100人中,优秀等级有75人,其优秀率为![]() ,可估计出参赛选手中优秀等级的选手人数,(3)这6名选手中任选3人总共有20种选法,有2名选手的等级为优秀共有6种选法,可计算出优秀的概率.
,可估计出参赛选手中优秀等级的选手人数,(3)这6名选手中任选3人总共有20种选法,有2名选手的等级为优秀共有6种选法,可计算出优秀的概率.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,且D,E分别是棱A1B1 , A1A1的中点,点F在棱AB上,且AF= ![]() AB.
AB.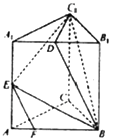
(1)求证:EF∥平面BDC1;
(2)求三棱锥D﹣BEC1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知曲线 ![]() (α为参数),在以O为极点,x轴正半轴为极轴的极坐标系中,曲线
(α为参数),在以O为极点,x轴正半轴为极轴的极坐标系中,曲线 ![]() ,曲线C3:ρ=2sinθ.
,曲线C3:ρ=2sinθ.
(1)求曲线C1与C2的交点M的直角坐标;
(2)设点A,B分别为曲线C2 , C3上的动点,求|AB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=|ax﹣1|,若实数a>0,不等式f(x)≤3的解集是{x|﹣1≤x≤2}.
(Ⅰ)求a的值;
(Ⅱ)若 ![]() <|k|存在实数解,求实数k的取值范围.
<|k|存在实数解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有个名句“运筹帷幄之中,决胜千里之外”.其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如下表: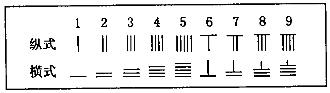
表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推,例如6613用算筹表示就是: ![]() ,则5288用算筹式可表示为( )
,则5288用算筹式可表示为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD, ![]() ,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF=1.
,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF=1.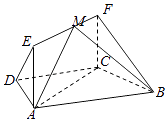
(1)求证:EF⊥平面BCF;
(2)点M在线段EF(含端点)上运动,当点M在什么位置时,平面MAB与平面FCB所成锐二面角最大,并求此时二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() +
+ ![]() =1的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
=1的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
(Ⅰ)当t=4,|AM|=|AN|时,求△AMN的面积;
(Ⅱ)当2|AM|=|AN|时,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com