
分析 若正数a,b满足f(3a+2b)<1,则0<3a+2b<6,画出满足条件的可行域,分析$\frac{b+1}{a-1}$的几何意义,数形结合可得答案.
解答 解:∵函数f(x)在x∈(0,+∞)单调递增,且f(6)=1,
若正数a,b满足f(3a+2b)<1,
则0<3a+2b<6,
满足条件的可行域如下图所示: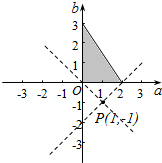
$\frac{b+1}{a-1}$表示可行域内(a,b)点与(1,-1)点连线的斜率,
由图可得:$\frac{b+1}{a-1}$的取值范围是(-∞,-1)∪(1,+∞),
故答案为:(-∞,-1)∪(1,+∞)
点评 本题考查的知识点是函数单调性的性质,线性规划,斜率公式,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | ($\frac{1}{6}$,+∞) | C. | (-∞,1) | D. | ($\frac{3}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
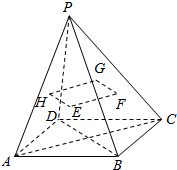 如图所示,已知四边形ABCD是平行四边形,P点是四边形ABCD所在平面外一点,连接PA、PB、PC、PD,设点E、F、G、H分别为△PAB、△PBC、△PCD、△PDA的重心.试用向量法证明E、F、G、H四点共面.
如图所示,已知四边形ABCD是平行四边形,P点是四边形ABCD所在平面外一点,连接PA、PB、PC、PD,设点E、F、G、H分别为△PAB、△PBC、△PCD、△PDA的重心.试用向量法证明E、F、G、H四点共面.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北石家庄一中高一下期末数学(理)试卷(解析版) 题型:选择题
已知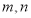 表示两条不同直线,
表示两条不同直线,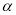 表示平面.下列说法正确的是
表示平面.下列说法正确的是
A.若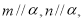 则
则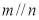 B.若
B.若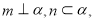 ,则
,则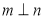
C.若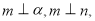 则
则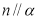 D.若
D.若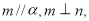 ,则
,则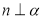
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com