
已知四面体 的棱长均为2,其正视图是边长为2的等边三角形(如图,其
的棱长均为2,其正视图是边长为2的等边三角形(如图,其
中 为水平线),则其侧视图的面积是
为水平线),则其侧视图的面积是
A. | B. | C. | D. |
A
解析考点:由三视图求面积、体积.
专题:图表型.
分析:由题意,四面体A-BCD的棱长均为2,此四面体是一个正四面体,其正视图是边长为2的等边三角形(如图,其中BC为水平线),即包含BC这一边的侧面是垂直于底面的,由此可得出其侧视图的形状,即它的度量,求出侧视图的面积,选出正确选项
解答: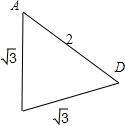 解:由题意四面体A-BCD的棱长均为2,其正视图是边长为2的等边三角形(如图,其中BC为水平线),可得此四面体是一个正四面体,且包含BC这一边的侧面是垂直于底面的,故此几何体的侧视图如图
解:由题意四面体A-BCD的棱长均为2,其正视图是边长为2的等边三角形(如图,其中BC为水平线),可得此四面体是一个正四面体,且包含BC这一边的侧面是垂直于底面的,故此几何体的侧视图如图
下利用海伦公式求三角形的面积
令a=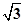 ,b=
,b=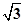 ,c=2,则p=
,c=2,则p=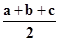 =
=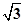 +1,
+1,
由公式S= =
= =
=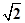
故选A
点评:本题考查由三视图求面积、体积,解答本题的关键是理解题意,得出侧视图的几何特征,是一个边长分别为 =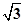 ,
, 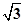 ,2的等腰三角形,本题由于正四面体放置的位置特殊,求解时要注意领会“BC为水平线”这句话的含义.
,2的等腰三角形,本题由于正四面体放置的位置特殊,求解时要注意领会“BC为水平线”这句话的含义.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com