
【题目】设![]() 是同一球面上的四点,
是同一球面上的四点,![]() 是边长为6的等边三角形,若三棱锥
是边长为6的等边三角形,若三棱锥![]() 体积的最大值为
体积的最大值为![]() ,则该球的表面积为( )
,则该球的表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
作出图形由图知,当点D与球心O以及△ABC外接圆圆心三点共线且D与△ABC外接圆圆心位于球心的异侧时,三棱锥D﹣ABC的体积取得最大值,结合三棱锥的体积求出棱锥的h,然后利用勾股定理求球O的半径R,最后利用表面积公式可求出答案.
如图所示,
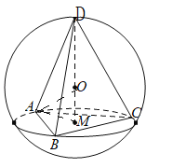
由题意可知,设点M为△ABC外接圆的圆心,当点D、O、M三点共线时,且D、M分别位于点O的异侧时,三棱锥D﹣ABC的体积取得最大值,
△ABC的面积为![]() ,
,
由于三棱锥D﹣ABC的体积的最大值为![]() ,得DM=6,
,得DM=6,
易知DM⊥平面ABC,则三棱锥D﹣ABC为正三棱锥,△ABC的外接圆直径为2AM=![]() ,∴AM=2
,∴AM=2![]() ,设球O的半径为为R,在直角三角形AOM中,
,设球O的半径为为R,在直角三角形AOM中,
由勾股定理得![]() ,即
,即![]() ,解得R=4或R=6(舍去)
,解得R=4或R=6(舍去)
因此,球O的表面积为![]() .
.
故选:A.


科目:高中数学 来源: 题型:
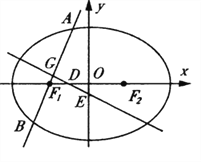
【题目】如图,已知椭圆![]() :
: ![]() , 其左右焦点为
, 其左右焦点为![]() 及
及![]() ,过点
,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
, ![]() 的中垂线与
的中垂线与![]() 轴和
轴和![]() 轴分别交于
轴分别交于![]() 两点,且
两点,且![]() 、
、![]() 、
、![]() 构成等差数列.
构成等差数列.
(1)求椭圆![]() 的方程;
的方程;
(2)记![]() 的面积为
的面积为![]() ,
, ![]() (
(![]() 为原点)的面积为
为原点)的面积为![]() ,试问:是否存在直线
,试问:是否存在直线![]() ,使得
,使得![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解我市参加2018年全国高中数学联赛的学生考试结果情况,从中选取60名同学将其成绩(百分制,均为正数)分成![]() 六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
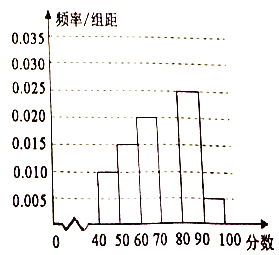
(1)求分数在![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)根据频率分布直方图,估计本次考试成绩的众数、均值;
(3)根据评奖规则,排名靠前10%的同学可以获奖,请你估计获奖的同学至少需要所少分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com