练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设随机变量X的分布列为P(X＝i)＝，(i＝1,2,3,4)．
    (1)求P(X＜3)；
    (2)求P；
    (3)求函数F(x)＝P(X＜x)．

    (1)   (2)    (3)

    解析解：(1)P(X＜3)＝P(X＝1)＋P(X＝2)＝.
    (2)P＝P(X＝1)＋P(X＝2)＋P(X＝3)＝
    (3)F(x)＝P(X＜x)＝

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    本着健康、低碳的生活理念，租自行车骑游的人越来越多．某自行车租车点的收费标准是每车每次租不超过两小时免费，超过两小时的收费标准为2元(不足1小时的部分按1小时计算)．有人独立来该租车点则车骑游．各租一车一次．设甲、乙不超过两小时还车的概率分别为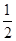，；两小时以上且不超过三小时还车的概率分别为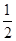，；两人租车时间都不会超过四小时．
    (1)求出甲、乙所付租车费用相同的概率；
    (2)求甲、乙两人所付的租车费用之和为随机变量X，求X的分布列与数学期望E(X)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知某种零件的尺寸X(单位：mm)服从正态分布，其正态曲线在(0,80)上是增函数，在(80，＋∞)上是减函数，且f(80)＝.
    (1)求正态分布密度函数的解析式；
    (2)估计尺寸在72mm～88mm之间的零件大约占总数的百分之几．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    对一批共50件的某电器进行分类检测，其重量（克）统计如下：

    重量段
    		[80，85）
    		[85，90）
    		[90，95）
    		[95，100]
    件数
    		5
    		a
    		15
    		b
    规定重量在82克及以下的为“A”型，重量在85克及以上的为“B”型，已知该批电器有“A”型2件
    （1）从该批电器中任选1件，求其为“B”型的概率；
    （2）从重量在［80,85)的5件电器中，任选2件，求其中恰有1件为“A”型的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图，由M到N的电路中有4个元件，分别标为T1，T2，T3，T4，电流能通过T1，T2，T3的概率都是p，电流能通过T4的概率是0.9.电流能否通过各元件相互独立．已知T1，T2，T3中至少有一个能通过电流的概率为0.999.

    (1)求p；
    (2)求电流能在M与N之间通过的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    从某批产品中，有放回地抽取产品二次，每次随机抽取1件，假设事件A“取出的2件产品都是二等品”的概率P(A)＝0.04
    (1)求从该批产品中任取1件是二等品的概率；
    (2)若该批产品共10件，从中任意抽取2件；X表示取出的2件产品中二等品的件数，求X的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    江西某品牌豆腐食品是经过、、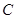三道工序加工而成的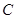，、、工序的产品合格率分别为、、．已知每道工序的加工都相互独立，三道工序加工的产品都为合格时产品为一等品；恰有两次合格为二等品；其它的为废品，不进入市场．
    （1）生产一袋豆腐食品，求产品为废品的概率；
    （2）生产一袋豆腐食品，设为三道加工工序中产品合格的工序数，求的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某市准备从5名报名者（其中男3人，女2人）中选2人参加两个副局长职务竞选.
    （1）求所选2人均为女副局长的概率；
    （2）若选派两个副局长依次到A、B两个局上任，求A局是男副局长的情况下，B局是女副局长的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设函数f(x)＝x2＋bx＋c，其中b、c是某范围内的随机数，分别在下列条件下，求事件A“f(1)≤5且f(0)≤3”发生的概率．
    (1)若随机数b，c∈{1，2，3，4}；
    (2)已知随机函数Rand()产生的随机数的范围为{x|0≤x≤1}，b，c是算法语句b＝4*Rand()和c＝4*Rand()的执行结果．(注：符号“*”表示“乘号”)

    查看答案和解析>>

    同步练习册答案