
【题目】如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,![]() ,四边形BDEF是矩形,平面
,四边形BDEF是矩形,平面![]() 平面ABCD,
平面ABCD,![]() ,H是CF的中点.
,H是CF的中点.

(1)求证:![]() 平面BDEF;
平面BDEF;
(2)求直线DH与平面CEF所成角的正弦值;
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 是自然对数的底数).
是自然对数的底数).
(1)若函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,试确定函数
,试确定函数![]() 的单调区间;
的单调区间;
(2)①当![]() ,
,![]() 时,若对于任意
时,若对于任意![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的最小值;②当
的最小值;②当![]() 时,设函数
时,设函数![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 是坐标原点.
是坐标原点.
(1)若直线![]() 过点
过点![]() 且
且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)已知点![]() ,若直线
,若直线![]() 不与坐标轴垂直,且
不与坐标轴垂直,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知F是抛物线C:![]() 的焦点,过E(﹣l,0)的直线
的焦点,过E(﹣l,0)的直线![]() 与抛物线分別交于A,B两点(点A,B在x轴的上方).
与抛物线分別交于A,B两点(点A,B在x轴的上方).
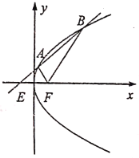
(1)设直线AF,BF的斜率分別为![]() ,
,![]() ,证明:
,证明:![]() ;
;
(2)若![]() ABF的面积为4,求直线
ABF的面积为4,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省确定从2021年开始,高考采用“![]() ”的模式,取消文理分科,即“3”包括语文、数学、英语,为必考科目:“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取
”的模式,取消文理分科,即“3”包括语文、数学、英语,为必考科目:“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含男生110人,求
名学生中含男生110人,求![]() 的值及抽取到的女生人数;
的值及抽取到的女生人数;
(2)学校计划在高二上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生讲行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目).下表是根据调查结果得到的
名学生讲行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目).下表是根据调查结果得到的![]() 列联表,请将列联表补充完整,并判断是否有
列联表,请将列联表补充完整,并判断是否有![]() 的把握认为选择科目与性别有关?说明你的理由;
的把握认为选择科目与性别有关?说明你的理由;
性别 | 选择物理 | 选择历史 | 总计 |
男生 | 50 | ||
女生 | 30 | ||
总计 |
(3)在(2)的条件下,从抽取的选择“物理”的学生中按分层抽样抽取6人,再从这6名学生中抽取2人,对“物理”的选课意向作深入了解,求2人中至少有1名女生的概率.
参考公式:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点![]() 是双曲线
是双曲线![]()
![]() 上的动点,
上的动点,![]() 是双曲线的焦点,M是
是双曲线的焦点,M是![]() 的平分线上一点,且
的平分线上一点,且![]() ,某同学用以下方法研究
,某同学用以下方法研究![]() :延长
:延长![]() 交
交![]() 于点N,可知
于点N,可知![]() 为等腰三角形,且M为
为等腰三角形,且M为![]() 的中点,得
的中点,得![]() ,类似地:点
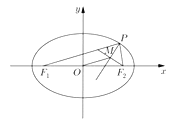
,类似地:点![]() 是椭圆
是椭圆![]()
![]() 上的动点,
上的动点,![]() 椭圆的焦点,M是
椭圆的焦点,M是![]() 的平分线上一点,且
的平分线上一点,且![]() 则
则![]() 的取值范围是______
的取值范围是______

查看答案和解析>>
科目:高中数学 来源: 题型:
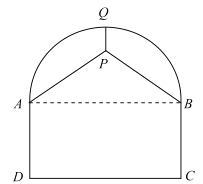
【题目】如图,某隧道的剖面图是由半圆及矩形![]() 组成,交通部门拟在隧道顶部安装通风设备(视作点
组成,交通部门拟在隧道顶部安装通风设备(视作点![]() ),为了固定该设备,计划除从隧道最高点
),为了固定该设备,计划除从隧道最高点![]() 处使用钢管垂直向下吊装以外,再在两侧自
处使用钢管垂直向下吊装以外,再在两侧自![]() 两点分别使用钢管支撑.已知道路宽
两点分别使用钢管支撑.已知道路宽![]() ,设备要求安装在半圆内部,所使用的钢管总长度为
,设备要求安装在半圆内部,所使用的钢管总长度为![]() .
.
(1)①设![]() ,将
,将![]() 表示为关于
表示为关于![]() 的函数;
的函数;
②设![]() ,将
,将![]() 表示为关于
表示为关于![]() 的函数;
的函数;
(2)请选用(1)中的一个函数关系式,说明如何设计,所用的钢管材料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.

(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com