
【题目】一排![]() 个空位,四人就坐其中的
个空位,四人就坐其中的![]() 个位子.
个位子.
(1)若每人左、右两边都有空位,有几种坐法?
(2)若![]() 个空位中,
个空位中,![]() 个相连,另
个相连,另![]() 个也相连,但
个也相连,但![]() 个不连在一起,有几种坐法?
个不连在一起,有几种坐法?
【答案】(1)![]() 种(2)
种(2)![]() 种
种
【解析】
(1)采用插空法,先将![]() 个空位摆好,再将坐着人的四个位子进行插空处理,进而得解;
个空位摆好,再将坐着人的四个位子进行插空处理,进而得解;
(2)将坐着人的四个位子全排列,将![]() 个空位“捆绑”,另2个空位也“捆绑”,然后进行插空处理,进而得解.
个空位“捆绑”,另2个空位也“捆绑”,然后进行插空处理,进而得解.
(1)每人左、右两边都有空位,即四人不能相邻,属于“不相邻问题”,
用“插空法”求解:先将![]() 个空位摆好,因为空位无区别,所以这
个空位摆好,因为空位无区别,所以这![]() 个空位不必排列,然后将坐着人的四个位子插到
个空位不必排列,然后将坐着人的四个位子插到![]() 个空位所形成的
个空位所形成的![]() 个空档里,所以有
个空档里,所以有![]() 种坐法,
种坐法,
所以,若每人左、右两边都有空位,有![]() 种坐法.
种坐法.
(2)先将坐着人的四个位子排好顺序,再将![]() 个空位“捆绑”,另2个空位也“捆绑”,然后插入到坐好
个空位“捆绑”,另2个空位也“捆绑”,然后插入到坐好![]() 个人的位子中间或两旁,所以共有
个人的位子中间或两旁,所以共有![]() 种坐法,
种坐法,
所以,若![]() 个空位中,
个空位中,![]() 个相连,另
个相连,另![]() 个也相连,但
个也相连,但![]() 个不连在一起,有
个不连在一起,有![]() 种坐法.
种坐法.


科目:高中数学 来源: 题型:
【题目】双曲线C的渐近线方程为![]() ,一个焦点为F(0,﹣8),则该双曲线的标准方程为_____.已知点A(﹣6,0),若点P为C上一动点,且P点在x轴上方,当点P的位置变化时,△PAF的周长的最小值为_____.
,一个焦点为F(0,﹣8),则该双曲线的标准方程为_____.已知点A(﹣6,0),若点P为C上一动点,且P点在x轴上方,当点P的位置变化时,△PAF的周长的最小值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() 的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且
的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且![]() .
.
(1)求抛物线C的方程;
(2)过F的直线l与C相交于A,B两点,若AB的垂直平分线![]() 与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在某海岸P的附近有三个岛屿Q,R,S,计划建立三座独立大桥,将这四个地方连起来,每座桥只连接两个地方,且不出现立体交叉形式,则不同的连接方式有( ).
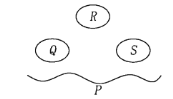
A.24种B.20种C.16种D.12种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD与△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
①![]() ;
;
②∠BAC=60°;
③三棱锥D﹣ABC是正三棱锥;
④平面ADC的法向量和平面ABC的法向量互相垂直.
其中正确结论的序号是 .(请把正确结论的序号都填上)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在30瓶饮料中,有3瓶已过了保质期.从这30瓶饮料中任取2瓶,则至少取到一瓶已过保质期的概率为 _________ .(结果用最简分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某段城铁线路上依次有![]() 、
、![]() 、
、![]() 三站,
三站,![]() ,
,![]() ,在列车运行时刻表上,规定列车
,在列车运行时刻表上,规定列车![]() 时整从
时整从![]() 站出发,
站出发,![]() 时
时![]() 分到达
分到达![]() 站并停车
站并停车![]() ,
,![]() 时
时![]() 分到达
分到达![]() 站,在实际运行时,假设列车从
站,在实际运行时,假设列车从![]() 站正点出发,在
站正点出发,在![]() 站停留
站停留![]() ,并在行驶时以同一速度
,并在行驶时以同一速度![]() 匀速行驶,列车从
匀速行驶,列车从![]() 站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差.
站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差.
(1)分别写出列车在![]() 、
、![]() 两站的运行误差;
两站的运行误差;
(2)若要求列车在![]() 、
、![]() 两站的运行误差之和不超过
两站的运行误差之和不超过![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全民健身旨在全面提高国民体质和健康水平,倡导全民做到每天参加一次以上的健身活动,学会两种以上健身方法,每年进行一次体质测定.为响应全民健身号召,某单位在职工体测后就某项健康指数(百分制)随机抽取了30名职工的体测数据作为样本进行调查,具体数据如茎叶图所示,其中有1名女职工的健康指数的数据模糊不清(用x表示),已知这30名职工的健康指数的平均数为76.2.
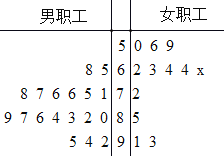
(1)根据茎叶图,求样本中男职工健康指数的众数和中位数;
(2)根据茎叶图,按男女用分层抽样从这30名职工中随机抽取5人,再从抽取的5人中随机抽取2人,求抽取的2人都是男职工的概率;
(3)经计算,样本中男职工健康指数的平均数为81,女职工现有数据(即剔除x)健康指数的平均数为69,方差为190,求样本中所有女职工的健康指数的平均数和方差(结果精确到0.1).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com