
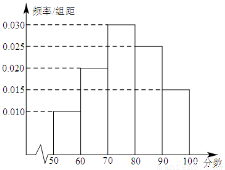
某中学从某次考试成绩中抽取若干名学生的分数,并绘制成如图所示的频率分布直方图,样本数据分组为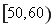 、
、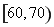 、
、 、
、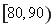 、
、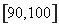 .若用分层抽样的方法从样本中抽取分数在
.若用分层抽样的方法从样本中抽取分数在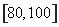 范围内的数据
范围内的数据 个,则其中分数在
个,则其中分数在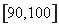 范围内的样本数据有( )
范围内的样本数据有( )
A.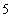 个 B.
个 B.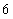 个 C.
个 C.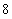 个 D.
个 D.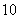 个
个
 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:解答题
现有甲、乙两个靶,某射手向甲靶射击一次,命中的概率为 ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击.
,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击.
(1)求该射手恰好命中一次的概率.
(2)求该射手的总得分X的分布列.
查看答案和解析>>
科目:高中数学 来源:2014年广东省广州市毕业班综合测试一理科数学试卷(解析版) 题型:解答题
甲、乙、丙三人参加某次招聘会,假设甲能被聘用的概率是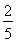 ,甲、丙两人同时不能被聘用的概率是
,甲、丙两人同时不能被聘用的概率是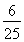 ,乙、丙两人同时能被聘用的概率为
,乙、丙两人同时能被聘用的概率为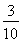 ,且三人各自能否被聘用相互独立.
,且三人各自能否被聘用相互独立.
(1)求乙、丙两人各自被聘用的概率;
(2)设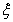 为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求
为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求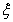 的分布列与均值(数学期望).
的分布列与均值(数学期望).
查看答案和解析>>
科目:高中数学 来源:2014年广东省广州市毕业班综合测试一文科数学试卷(解析版) 题型:解答题
已知双曲线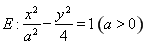 的中心为原点
的中心为原点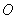 ,左、右焦点分别为
,左、右焦点分别为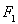 、
、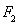 ,离心率为
,离心率为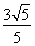 ,点
,点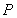 是直线
是直线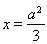 上任意一点,点
上任意一点,点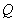 在双曲线
在双曲线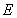 上,且满足
上,且满足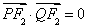 .
.
(1)求实数 的值;
的值;
(2)证明:直线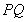 与直线
与直线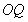 的斜率之积是定值;
的斜率之积是定值;
(3)若点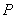 的纵坐标为
的纵坐标为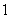 ,过点
,过点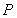 作动直线
作动直线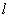 与双曲线右支交于不同的两点
与双曲线右支交于不同的两点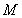 、
、 ,在线段
,在线段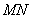 上去异于点
上去异于点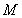 、
、 的点
的点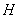 ,满足
,满足 ,证明点
,证明点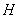 恒在一条定直线上.
恒在一条定直线上.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:解答题
如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BA=BC.把△BAC沿AC折起到△PAC的位置,使得点P在平面ADC上的正投影O恰好落在线段AC上,如图2所示.点E、F分别为棱PC,CD的中点.
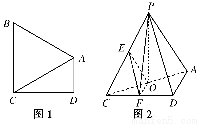
(1)求证:平面OEF∥平面APD;
(2)求证:CD⊥平面POF;
(3)在棱PC上是否存在一点M,使得M到P,O,C,F四点距离相等?请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:解答题
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数如下表:
| 1号 | 2号 | 3号 | 4号 | 5号 |
甲组 | 4 | 5 | x | 9 | 10 |
乙组 | 5 | 6 | 7 | y | 9 |
(1)已知两组技工在单位时间内加工的合格零件平均数为7,分别求出甲、乙两组技工在单位时间内加工的合格零件的方差,并由此分析两组技工的加工水平;
(2)质检部门从该车间甲、乙两组中各随机抽取一名技工,对其加工的零件进行检测,若2人加工的合格零件个数之和超过14,则称该车间“质量合格”,求该车间“质量合格”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com