
已知直线l:(2m+1)x+(m+1)y=7m+5,圆C:x2+y2-6x-8y+21=0.
⑴求证:直线l与圆C总相交;
⑵求相交弦的长的最小值及此时m的值.
⑴ 直线l的方程可变形为:(2x+y-7)m +(x+y-5)=0, 。。。。。。。。。。。。1分
令 得
得 ,即直线l过定点P(2,3). 。。。。。。。。。。。3分
,即直线l过定点P(2,3). 。。。。。。。。。。。3分
圆C:x2+y2-6x-8y+21=0 即(x-3)2+(y-4)2=4。。。。。。。。。。。。。。。。。。。。。。。4分
圆心C(3,4)半径r =2
∵ |CP|= 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。5分
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。5分
∴点P(2,3)在圆C内,则直线l与圆C总相交.。。。。。。。。。。。。。。。。。。。。。6分
⑵ 圆心C(3,4), P(2,3)
当CP⊥直线l时和定点(2,3),弦长最短。 。。。。。。。。。。。。。。。。。。8分
∵|CP|=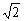 ,r =2
∴弦长|AB|=
,r =2
∴弦长|AB|= 。。。。。。。。。。。。10分
。。。。。。。。。。。。10分
此时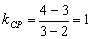 , ∴
, ∴ ,
,
则 ∴
∴ ; 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。12分
; 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。12分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:训练必修二数学人教A版 人教A版 题型:044
已知直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R)与圆C:x2+y2-2x-4y-20=0,
(1)求证:对任意实数m,l与圆C总有两个交点A、B;
(2)当|AB|取得最小值时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l:(2m+1)x+(m+1)y=7m+5,圆C:x2+y2-6x-8y+21=0.
⑴求证:直线l与圆C总相交;
⑵求相交弦的长的最小值及此时m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com