
【题目】已知点A(x1,f(x1)),B(x2,f(x2))是函数f(x)=2sin(ωx+φ)![]() 图象上的任意两点,且角φ的终边经过点
图象上的任意两点,且角φ的终边经过点![]() ,若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为
,若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为![]() .
.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间;
(3)当![]() 时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由![]() 角终边所过点求出
角终边所过点求出![]() ,从而确定
,从而确定![]() 角,由|x1﹣x2|的最小值确定函数的周期,从而确定
角,由|x1﹣x2|的最小值确定函数的周期,从而确定![]() ,得函数解析式;
,得函数解析式;
(2)由正弦函数的单调性可得f(x)的单调递增区间;
(3)先得出![]() 的范围,知
的范围,知![]() 大于0,因此恒成立的不等式可用分离参数法变为
大于0,因此恒成立的不等式可用分离参数法变为![]() ,因此只要求得
,因此只要求得![]() 的最大值即可得
的最大值即可得![]() 的取值范围.
的取值范围.
(1)角φ的终边经过点![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
由|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为![]() ,得
,得![]() ,
,
即![]() ,∴ω=3
,∴ω=3
∴![]()
(2)由![]() ,
,
可得![]() ,
,
∴函数f(x)的单调递增区间为![]() ,k∈z
,k∈z
(3 ) 当![]() 时,
时,![]() ,
,
于是,2+f(x)>0,
∴mf(x)+2m≥f(x)等价于![]()
由![]() ,得
,得![]() 的最大值为
的最大值为![]()
∴实数m的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上一点.
上一点.

(I)求证: ![]() .
.
(II)若![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() .
.
(III)若二面角![]() 的大小为
的大小为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某印刷厂为了研究单册书籍的成本![]() (单位:元)与印刷册数
(单位:元)与印刷册数![]() (单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
印刷册数 |
|
|
|
|
|
单册成本 |
|
|
|
|
|
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到![]() );
);
印刷册数 |
|
|
|
|
| |
单册成本 |
|
|
|
|
| |
模型甲 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
模型乙 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
②分别计算模型甲与模型乙的残差平方和,并通过比较,判断哪个模型拟合效果更好.
(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷,根据市场调查,新需求量为![]() 千册,若印刷厂以每册
千册,若印刷厂以每册![]() 元的价格将书籍出售给订货商,求印刷厂二次印刷
元的价格将书籍出售给订货商,求印刷厂二次印刷![]() 千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 同时满足下列两个条件,则称该函数为“和谐函数”:
同时满足下列两个条件,则称该函数为“和谐函数”:
(1)任意![]() 恒成立;
恒成立;
(2)任意![]() 且
且![]() ,都有
,都有![]()
以下四个函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 中是“和谐函数”的为________________(写出所有正确的题号).
中是“和谐函数”的为________________(写出所有正确的题号).
查看答案和解析>>
科目:高中数学 来源: 题型:
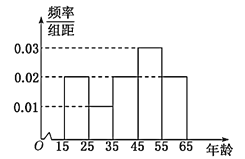
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”.为了了解人们]对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15∽65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率.
②记抽到45岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在单位正方体![]() 中,点P在线段
中,点P在线段![]() 上运动,给出以下四个命题:
上运动,给出以下四个命题:

![]() 异面直线
异面直线![]() 与
与![]() 间的距离为定值;
间的距离为定值;
![]() 三棱锥
三棱锥![]() 的体积为定值;
的体积为定值;
![]() 异面直线
异面直线![]() 与直线
与直线![]() 所成的角为定值;
所成的角为定值;
![]() 二面角
二面角![]() 的大小为定值.
的大小为定值.
其中真命题有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com