
����Ŀ��ijʳƷ��Ϊ�˼��ס��������Զ���װ��ˮ�ߵ�����������������������ˮ���ϸ���ȡ40����Ʒ��Ϊ���������Ƴ����ǵ���������λ���ˣ�������ֵ����![]() �ڵIJ�ƷΪ�ϸ�Ʒ������Ϊ���ϸ�Ʒ.
�ڵIJ�ƷΪ�ϸ�Ʒ������Ϊ���ϸ�Ʒ.
ע����1�Ǽ���ˮ��������Ƶ���ֲ�����ͼ1������ˮ��������Ƶ�ʷֲ�ֱ��ͼ.
��Ʒ�������ˣ� | Ƶ�� |
| 6 |
| 8 |
| 14 |
| 8 |
| 4 |
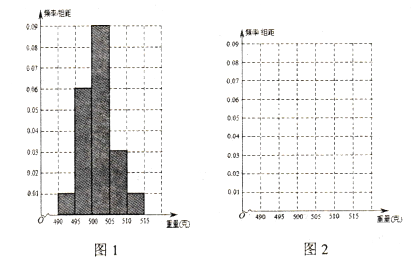
��1�����������1�е�������ͼ2����������ˮ��������Ƶ�ʷֲ�ֱ��ͼ��
��2������Ƶ����Ϊ���ʣ��Թ��ƴ�������ˮ���Ϸֱ���ȡ1����Ʒ���ò�Ʒǡ���Ǻϸ�Ʒ�ĸ��ʷֱ��Ƕ��٣�
��3��������ͳ�������������![]() �����������ش��ж��İ�����Ϊ��Ʒ�İ�װ�����������Զ���װ��ˮ�ߵ�ѡ���й�.
�����������ش��ж��İ�����Ϊ��Ʒ�İ�װ�����������Զ���װ��ˮ�ߵ�ѡ���й�.
����ˮ�� | ����ˮ�� | �ϼ� | |
�ϸ� | |||
���ϸ� | |||
�ϼ� |
�ο���ʽ��![]() ������
������![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡���1������������2���Ӽ���ˮ������ȡ1����Ʒ���ò�Ʒǡ���Ǻϸ�Ʒ�ĸ���Ϊ![]() ��������ˮ������ȡ1����Ʒ���ò�Ʒǡ���Ǻϸ�Ʒ�ĸ���Ϊ0.9.��3��������
��������ˮ������ȡ1����Ʒ���ò�Ʒǡ���Ǻϸ�Ʒ�ĸ���Ϊ0.9.��3��������
��������
��1������������ÿһ���Ƶ���������������ÿһ���Ƶ�ʣ�����Ƶ�ʷֲ�ֱ��ͼ��
��2�����������������еĺϸ�Ʒ���������������������ϸ�Ʒ��Ƶ�ʣ��ɹ��ƴ�������ˮ������ȡһ����Ʒ�ò�ƷΪ�ϸ�Ʒ�ĸ��ʣ�
��3���������������ݣ��г������������������Ĺ۲�ֵ�Ĺ�ʽ��������������۲�ֵ��ͬ�ٽ�ֵ���бȽϣ��õ���90%�İ�����Ϊ��Ʒ�İ�װ�����������Զ���װ��ˮ�ߵ�ѡ���йأ�
��1������ˮ��������Ƶ�ʷֲ�ֱ��ͼ���£�

��2���ɱ�1֪����ˮ�������кϸ�Ʒ��Ϊ![]() ��
��
�ʼ���ˮ�������кϸ�Ʒ��Ƶ��Ϊ![]() ��
��
��ͼ1֪����ˮ�������кϸ�Ʒ��Ƶ��Ϊ![]() ��
��
�ݴ˿ɹ��ƴӼ���ˮ������ȡ1����Ʒ���ò�Ʒǡ���Ǻϸ�Ʒ�ĸ���Ϊ![]() ��
��
������ˮ������ȡ1����Ʒ���ò�Ʒǡ���Ǻϸ�Ʒ�ĸ���Ϊ0.9.
��3���ɣ�2��֪����ˮ�������кϸ�Ʒ��Ϊ30������ˮ�������кϸ�Ʒ��Ϊ![]() .
.
![]() ���������£�
���������£�
����ˮ�� | ����ˮ�� | �ϼ� | |
�ϸ� | 30 | 36 | 66 |
���ϸ� | 10 | 4 | 14 |
�ϼ� | 40 | 40 | 80 |
��![]() ��
��
����![]() �İ�����Ϊ��Ʒ�İ�װ�����������Զ���װ��ˮ�ߵ�ѡ���й�.
�İ�����Ϊ��Ʒ�İ�װ�����������Զ���װ��ˮ�ߵ�ѡ���й�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �У�����
�У�����![]() Ϊ�������Σ�
��������![]() ��
��![]() ��
��![]() ��
��![]() �A����
�A����![]() .
.
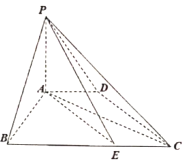
��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��ƽ�潻
��ƽ�潻![]() �ڵ�
�ڵ�![]() ����ƽ��
����ƽ��![]() ������
������![]() �ֳ������ȵ������֣�������
�ֳ������ȵ������֣�������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() .
.
��1�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����������![]() ��
��![]() ʱ������ʽ
ʱ������ʽ![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У���֪��ֱ��
�У���֪��ֱ��![]() �IJ������̣�
�IJ������̣�![]() ����
����![]() ������
Ϊ������![]() �� ��������ԭ��Ϊ���㣬
�� ��������ԭ��Ϊ���㣬![]() ���������Ϊ���Ὠ��������ϵ������
���������Ϊ���Ὠ��������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .
.
����������![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
������ֱ��![]() ������
������![]() ǡ����2��������ʱ����ֱ��
ǡ����2��������ʱ����ֱ��![]() ��һ�㷽��.
��һ�㷽��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��![]() ����ͼ����
����ͼ����![]() ���ҹ���ֱ��
���ҹ���ֱ��![]() �Գƣ������н�����ȷ���ǣ� ��
�Գƣ������н�����ȷ���ǣ� ��
A. ![]() ��
��![]() ���Ǽ�����
���Ǽ�����
B. ��������С������Ϊ![]()
C. ![]() �Ľ⼯��
�Ľ⼯��![]() ��
��![]()
D. ![]() ��һ���Գ�������
��һ���Գ�������![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����n��������ȵ������������������������ж����ٴ�����������ʹ������һ����������һ��.��n����Сֵ��ʹ������n������һ������������������һ���ܱ������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪��Բ
�У���֪��Բ![]() ����
����![]() ����������
����������![]() .
.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2��ֱ��![]() ��б��Ϊ
��б��Ϊ![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() ����������ֵ.
����������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() �ǹ���
�ǹ���![]() �н�Ϊ
�н�Ϊ![]() ������ֱ�ߣ�����Բ��Ϊ
������ֱ�ߣ�����Բ��Ϊ![]() ���뾶��Ϊ
���뾶��Ϊ![]() ��Բ�ֱ����У���Բ����һ��
��Բ�ֱ����У���Բ����һ��![]() ��
��![]() ��
��![]() �ľ���ֱ�Ϊ
�ľ���ֱ�Ϊ![]() ��
��![]() ����ô
����ô![]() ����СֵΪ��____����
����СֵΪ��____����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com