
【题目】判断下列命题的真假:
(1)存在两个无理数,它们的乘积是有理数;
(2)如果实数集的子集A是有限集,则A中的元素一定有最大值;
(3)没有一个无理数不是实数;
(4)如果一个四边形的对角线相等,则这个四边形是矩形;
(5)集合A是集合![]() 的子集;
的子集;
(6)集合![]() 是集合A的子集.
是集合A的子集.
 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如下:

每名快递员完成一件货物投递可获得的劳务费情况如下:
甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.
(1)根据表中数据写出甲公司员工![]() 在这10天投递的快递件数的平均数和众数;
在这10天投递的快递件数的平均数和众数;
(2)为了解乙公司员工![]() 的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为
的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为![]() (单位:元),求
(单位:元),求![]() 的概率;
的概率;
(3)根据表中数据估算公司的每位员工在该月所得的劳务费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)从某校高一年级随机抽取![]() 名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
组号 | 分组 | 频数 | 频率 |
|
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
|

(Ⅰ)求![]() 的值.
的值.
(Ⅱ)若![]() ,补全表中数据,并绘制频率分布直方图.
,补全表中数据,并绘制频率分布直方图.
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,若上述数据的平均值为![]() ,求
,求![]() ,
,![]() 的值,并由此估计该校高一学生的日平均睡眠时间不少于
的值,并由此估计该校高一学生的日平均睡眠时间不少于![]() 小时的概率.
小时的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上存在导数f′(x),对任意的x∈R,有f(x)+f(-x)=x2,且x∈(0,+∞)时,f′(x)<x.若f(1-a)-f(a)≥![]() -a,则实数a的取值范围是______.
-a,则实数a的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,在矩形
,在矩形![]() 中,
中, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起到
折起到![]() ,使得平面
,使得平面![]() 平面
平面![]() (如图
(如图![]() ).
).


图1 图2
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂因排污比较严重,决定着手整治,一个月时污染度为![]() ,整治后前四个月的污染度如下表:
,整治后前四个月的污染度如下表:
月数 |
|
|
|
| … |
污染度 |
|
|
|
| … |
污染度为![]() 后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 表示月数,
表示月数,![]() 、
、![]() 、
、![]() 分别表示污染度.
分别表示污染度.
(1)问选用哪个函数模拟比较合理,并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上周某校高三年级学生参加了数学测试,年级组织任课教师对这次考试进行成绩分析现从中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组;第二组;……;第六组,并据此绘制了如图所示的频率分布直方图.
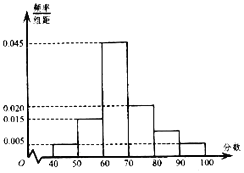
(1)估计这次月考数学成绩的平均分和众数;
(2)从成绩大于等于80分的学生中随机选2名,求至少有1名学生的成绩在区间![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com