
【题目】若直线l的极坐标方程为![]() ,曲线C的参数方程为
,曲线C的参数方程为![]() (
(![]() 为参数).
为参数).
![]() 若曲线上存在M,N两点关于直线l对称,求实数m的值;
若曲线上存在M,N两点关于直线l对称,求实数m的值;
![]() 若直线与曲线相交于P,Q两点,且
若直线与曲线相交于P,Q两点,且![]() ,求实数m的取值范围.
,求实数m的取值范围.
科目:高中数学 来源: 题型:
【题目】
已知等差数列![]() 的公差为
的公差为![]() ,前
,前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() 与前
与前![]() 项和
项和![]() ;
;
(2)将数列![]() 的前四项抽取其中一项后,剩下三项按原来顺序恰为等比数列
的前四项抽取其中一项后,剩下三项按原来顺序恰为等比数列![]() 的前三项,记数列
的前三项,记数列![]() 的前
的前![]() 项和为
项和为![]() ,若存在
,若存在![]() ,使得对任意
,使得对任意![]() ,总有
,总有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程![]() ,变量x增加一个单位时,y平均增加5个单位;
,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程![]() 必过(
必过(![]() );
);
④在一个2×2列联中,由计算得![]() 则有99%的把握确认这两个变量间有关系;
则有99%的把握确认这两个变量间有关系;
` 其中错误的个数是 ( )
本题可以参考独立性检验临界值表:
| 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.535 | 7.879 | 10.828 |
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“十三五”规划确定了到2020年消除贫困的宏伟目标,打响了精准扶贫的攻坚战,为完成脱贫任务,某单位在甲地成立了一家医疗器械公司吸纳附近贫困村民就工,已知该公司生产某种型号医疗器械的月固定成本为20万元,每生产1千件需另投入5.4万元,设该公司一月内生产该型号医疗器械x千件且能全部销售完,每千件的销售收入为![]() 万元,已知
万元,已知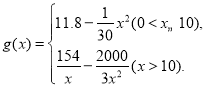
(1)请写出月利润y(万元)关于月产量x(千件)的函数解析式;
(2)月产量为多少千件时,该公司在这一型号医疗器械的生产中所获月利润最大?并求出最大月利润(精确到0.1万元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区消费者协会为了解本社区居民网购消费情况,随机抽取了100位居民作为样本,就最近一年来网购消费金额(单位:千元),网购次数和支付方式等进行了问卷调查.经统计这100位居民的网购消费金额均在区间![]() 内,按
内,按![]() 分成6组,其频率分布直方图如图所示.
分成6组,其频率分布直方图如图所示.
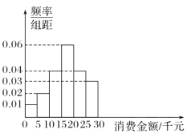
(1)估计该社区居民最近一年来网购消费金额的中位数;
(2)将网购消费金额在20千元以上者称为“网购迷”,补全下面的![]() 列联表,并判断有多大把握认为“网购迷与性别有关系”
列联表,并判断有多大把握认为“网购迷与性别有关系”
男 | 女 | 总计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
总计 | 100 |
附:![]() .
.
临界值表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果函数![]() 的导函数为
的导函数为![]() ,在区间
,在区间![]() 上存在
上存在![]() ,
,![]() 使得
使得![]() ,
,![]() ,则称
,则称![]() 为区间
为区间![]() 上的“双中值函数“
上的“双中值函数“![]() 已知函数
已知函数![]() 是
是![]() 上的“双中值函数“,则实数m的取值范围是
上的“双中值函数“,则实数m的取值范围是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面四边形
,底面四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点.
上一点.
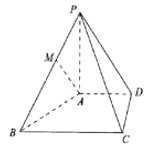
(1)若![]() ,则在线段
,则在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请确定
?若存在,请确定![]() 点的位置;若不存在,请说明理由
点的位置;若不存在,请说明理由
(2)己知![]() ,若异面直线
,若异面直线![]() 与
与![]() 成
成![]() 角,二而角
角,二而角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com