
分析 (1)代入可得
(2)求出g(x)=(2-t)($\frac{1}{2}$)x+(t-3)($\frac{1}{2}$)2xd配方得:=(t-3)[($\frac{1}{2}$)x+$\frac{2-t}{2(t-3)}$]2-$\frac{(2-t)^{2}}{4(t-3)}$,分别对t进行分类讨论可得函数的最小值;
(3)式子整理为t(2x-1)<2x+1-3,由t∈[-1,1],要使恒成立,则2x+1-3>2x-1且2x+1-3>-2x+1,分别求解求出x的范围.
解答 解:(1)f(0)=(2-t)+t-3
=-1;
(2)g(x)=(2-t)($\frac{1}{2}$)x+(t-3)($\frac{1}{2}$)2x
=(t-3)[($\frac{1}{2}$)2x+$\frac{2-t}{t-3}$]
=(t-3)[($\frac{1}{2}$)x+$\frac{2-t}{2(t-3)}$]2-$\frac{(2-t)^{2}}{4(t-3)}$
对称轴为x=-$\frac{2-t}{2(t-3)}$,($\frac{1}{2}$)x∈[$\frac{1}{2}$,1]
当3≤t≤4时,g(x)min=-$\frac{(2-t)^{2}}{4(t-3)}$
当t≥4时,g(x)min=g(1)=-1
当t<3时,g(x)min=g($\frac{1}{2}$)=2t-8;
(3)2x+1-t2x+t-3>0
∴t(2x-1)<2x+1-3
∵t∈[-1,1]
∴2x+1-3>2x-1且2x+1-3>-2x+1
解得x>$lo{g}_{2}\frac{4}{3}$且x>1
故x的范围为x>1.
点评 考察了二次函数的配方,参数的讨论以及对恒成立问题的理解.


科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
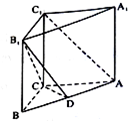 在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.
在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com