【题目】在平面直角坐标系
中，圆
：
，
，
，
为平面内一动点，若以线段
为直径的圆与圆相切．
（1）证明
为定值，并写出点的轨迹方程；
（2）设点的轨迹为曲线
，直线
过
交于
，
两点，过且与垂直的直线与交于
，
两点，求四边形
面积的取值范围．
【答案】(1)证明见解析，轨迹方程为
．(2)
.
【解析】分析：第一问结合题中条件画出相应的图形，连接相关线段，利用中位线的长度以及两圆内切时对应两圆心之间的距离与半径的关系，求得
，从而得到其为定值，之后借助于其范围，利用椭圆的定义，求得其轨迹方程；第二问分直线的斜率不存在、为零、存在且不为零三种情况来分析对应的四边形的面积，从而求得其范围.
详解：（1）设
的中点为
，连接
，
，
在
中，
，分别为
，的中点，所以
，
又圆与动圆相切，则
，所以
，即为定值，
，
所以点
的轨迹是以
，
为焦点的椭圆，
设椭圆方程为
，则
，
，
，
所以点的轨迹方程为．
（2）①当直线
的斜率不存在时，不妨设
，
，
，
，则
，
，四边形
面积
；
②当直线的斜率为0时，同理可得四边形面积
；
③当直线的斜率存在且不为0时，
可设直线的方程为
，设
，
，
联立
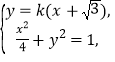得
，
，
，
，
同理
，
四边形面积
，设
，
则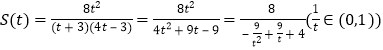
，
所以
；
综上所述，四边形面积的取值范围是．
名师点睛字词句段篇系列答案科目：高中数学 来源： 题型：
【题目】已知点
，直线
：
，
为平面上的动点，过点作直线的垂线，垂足为
，且满足
．
（1）求动点的轨迹
的方程；
（2）过点
作直线
与轨迹交于
，
两点，
为直线上一点，且满足
，若
的面积为
，求直线的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知海岛
在海岛
北偏东
，，相距
海里，物体甲从海岛以
海里/小时的速度沿直线向海岛移动，同时物体乙从海岛沿着海岛北偏西
方向以
海里/小时的速度移动．
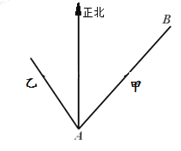
（1）问经过多长时间，物体甲在物体乙的正东方向；
（2）求甲从海岛到达海岛的过程中，甲、乙两物体的最短距离．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于定义域为D的函数y=f（x），如果存在区间[m，n]
D，同时满足：
①f（x）在[m，n]内是单调函数；
②当定义域是[m，n]时，f（x）的值域也是[m，n]．则称[m，n]是该函数的“和谐区间”．
（1）证明：[0，1]是函数y=f（x）=x2的一个“和谐区间”．
（2）求证：函数
不存在“和谐区间”．
（3）已知：函数
（a∈R，a≠0）有“和谐区间”[m，n]，当a变化时，求出n﹣m的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2018年4月4日召开的国务院常务会议明确将进一步推动网络提速降费工作落实，推动我国数字经济发展和信息消费，今年移动流量资费将再降30%以上，为响应国家政策，某通讯商计划推出两款优惠流量套餐，详情如下：
套餐名称 | 月套餐费/元 | 月套餐流量/M |
A | 30 | 3000 |
B | 50 | 6000 |
这两款套餐均有以下附加条款：套餐费用月初一次性收取，手机使用流量一旦超出套餐流量，系统就会自动帮用户充值2000M流量，资费20元；如果又超出充值流量，系统再次自动帮用户充值2000M流量，资费20元，以此类推。此外，若当月流量有剩余，系统将自动清零，不可次月使用。
小张过去50个月的手机月使用流量（单位：M）的频数分布表如下：
月使用流量分组 | [2000,3000] | (3000,4000] | (4000,5000] | (5000,6000] | (6000,7000] | (7000,8000] |
频数 | 4 | 5 | 11 | 16 | 12 | 2 |
根据小张过去50个月的手机月使用流量情况，回答以下几个问题：
（1）若小张选择A套餐，将以上频率作为概率，求小张在某一个月流量费用超过50元的概率.
（2）小张拟从A或B套餐中选定一款，若以月平均费用作为决策依据，他应订购哪一种套餐？说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
