
【题目】如图,已知在算法中“![]() ”和“
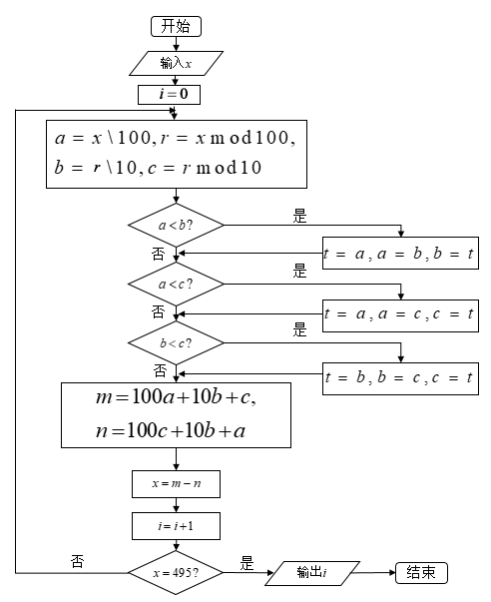
”和“![]() ”分别表示取商和取余数.为了验证三位数卡普雷卡尔“数字黑洞”(即输入一个无重复数字的三位数,经过如图的有限次的重排求差计算,结果都为495).小明输入
”分别表示取商和取余数.为了验证三位数卡普雷卡尔“数字黑洞”(即输入一个无重复数字的三位数,经过如图的有限次的重排求差计算,结果都为495).小明输入![]() ,则输出的
,则输出的![]() ( )
( )![]()
A.3B.4C.5D.6
【答案】B
【解析】
首先读懂程序,输入任意一个无重复数字的三位数,将其个位,十位,百位重新排列,组成一个最大数和一个最小数,写出每次循环的结果,使差是495结束循环,即可得出答案.
先读懂程序:输入任意一个无重复数字的三位数,
将其个位,十位,百位重新排列,组成一个最大数和一个最小数,
然后作差,若差不为495,则继续此过程,经过有限次步骤之后,最后结果一定是495.
对于输入的325,第一次循环:
重新排列后,最大数为532,最小数为235,相减得297,然后![]() ;
;
第二次循环:重新排列后,最大数为972,最小数为279,相减得693,然后![]() ;
;
第三次循环:重新排列后,最大数为963,最小数为369,相减得594,然后![]() ;
;
第四次循环:重新排列后,最大数为954,最小数为459,相减得495,然后![]() ,
,
结束循环,
故选:B.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:
【题目】设有编号分别为1,2,3,4,5,6,7,8的八个小球和编号为1,2,3,4,5,6,7,8的八个盒子.现将这八个小球随机放入八个盒子内,要求每个盒子内放一个球,要求编号为偶数的小球在编号为偶数的盒子内,且至少有四个小球在相同编号的盒子内,则一共有______种投放方法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知在算法中“![]() ”和“
”和“![]() ”分别表示取商和取余数.为了验证三位数卡普雷卡尔“数字黑洞”(即输入一个无重复数字的三位数,经过如图的有限次的重排求差计算,结果都为495).小明输入
”分别表示取商和取余数.为了验证三位数卡普雷卡尔“数字黑洞”(即输入一个无重复数字的三位数,经过如图的有限次的重排求差计算,结果都为495).小明输入![]() ,则输出的
,则输出的![]() ( )
( )![]()

A.3B.4C.5D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,在
,在![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,四边形
的中点,四边形![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() .
.

(Ⅰ)求异面直线![]() 与
与![]() 所成角的正弦值;
所成角的正弦值;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,且过点
,且过点![]() .
.
(1)求C的方程;
(2)若直线l与C有且只有一个公共点,l与圆x2+y2=6交于A,B两点,直线OA,OB的斜率分别记为k1,k2.试判断k1k2是否为定值,若是,求出该定值;否则,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,PA⊥底面ABCD,AD∥BC,AB=AC=AD=3,PA=BC=4.
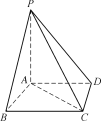
(1)求异面直线PB与CD所成角的余弦值;
(2)求平面PAD与平面PBC所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() ,
, ![]() ,
, ![]() 分别为椭圆的右顶点、上顶点和右焦点,且
分别为椭圆的右顶点、上顶点和右焦点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() :
: ![]() 被圆
被圆![]() :
: ![]() 所截得的弦长为
所截得的弦长为![]() ,若直线
,若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com